Parallelogram
A parallelogram is a quadrilateral where the opposite sides are equal in length and parallel.
The figure can be seen as a "slanted rectangle".
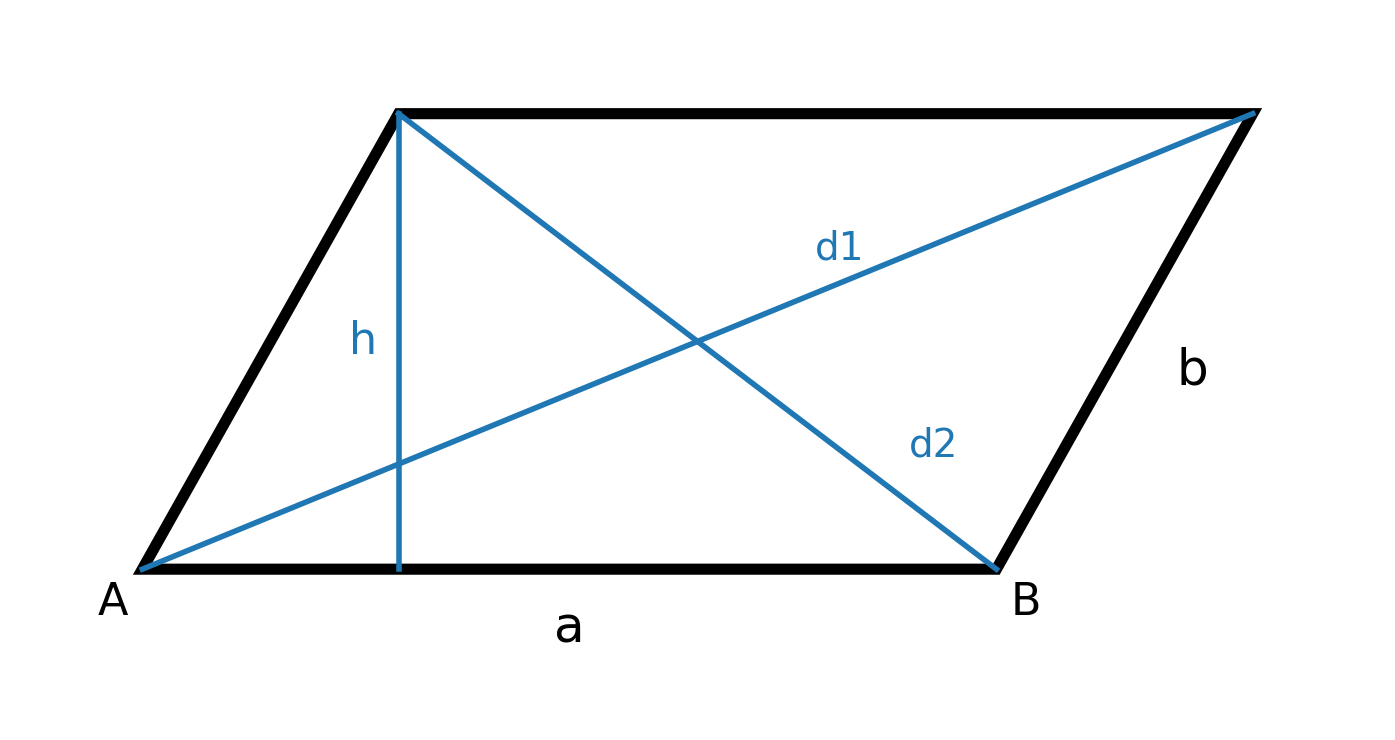
There are no right angles in a parallelogram, but the opposite angles are always equal. The sum of two adjacent angles is 180°.
$$ \large \angle A + \angle B = 180^\circ $$
A special variation of the parallelogram is called a rhombus. Here all four sides are equal in length. In the same way as an equilateral rectangle is called a square.
The intersection point of the diagonals in a parallelogram is also their midpoint.
This means that the diagonals divide each other into two equal parts, but they are not necessarily perpendicular.
Properties of a parallelogram
- Opposite sides are equal in length.
- Opposite sides are parallel.
- Opposite angles are equal.
- Adjacent angles add up to 180°.
- The intersection point of the diagonals is also their midpoint.
- A parallelogram can be divided into two congruent triangles along a diagonal.
When calculating with a parallelogram, it is often necessary to use trigonometry and triangle calculations.