Gauss' area formula (Shoelace formula)

Gauss' area formula is a method to calculate the area of an arbitrary polygon from the coordinates of its vertices. The method only requires knowledge of the points' coordinates in the plane.

The formula works for polygons described by points \( (x_1,y_1), (x_2,y_2), \ldots, (x_n,y_n) \), taken either clockwise or counterclockwise.

 

 

Formula

The area of a polygon with \( \large n \) vertices is:

 

$$ \large A = \frac{1}{2} \left| \sum_{i=1}^{n} \big( x_i \cdot y_{i+1} - x_{i+1} \cdot y_i \big) \right| $$

 

Here \( \large (x_{n+1}, y_{n+1}) = (x_1, y_1) \), so the last point connects back to the first.

 

 

Example 1: Triangle

Find the area of the triangle with points \( \large (0,0), (4,0), (4,3) \).

 

Insert into the formula:

 

$$ \large A = \frac{1}{2} \left| 0 \cdot 0 + 4 \cdot 3 + 4 \cdot 0 - \big( 0 \cdot 4 + 0 \cdot 4 + 3 \cdot 0 \big) \right| $$

$$ \large A = \frac{1}{2} \cdot 12 = 6 $$

 

The area is 6, which matches \( \large \frac{1}{2} \cdot 4 \cdot 3 = 6 \).

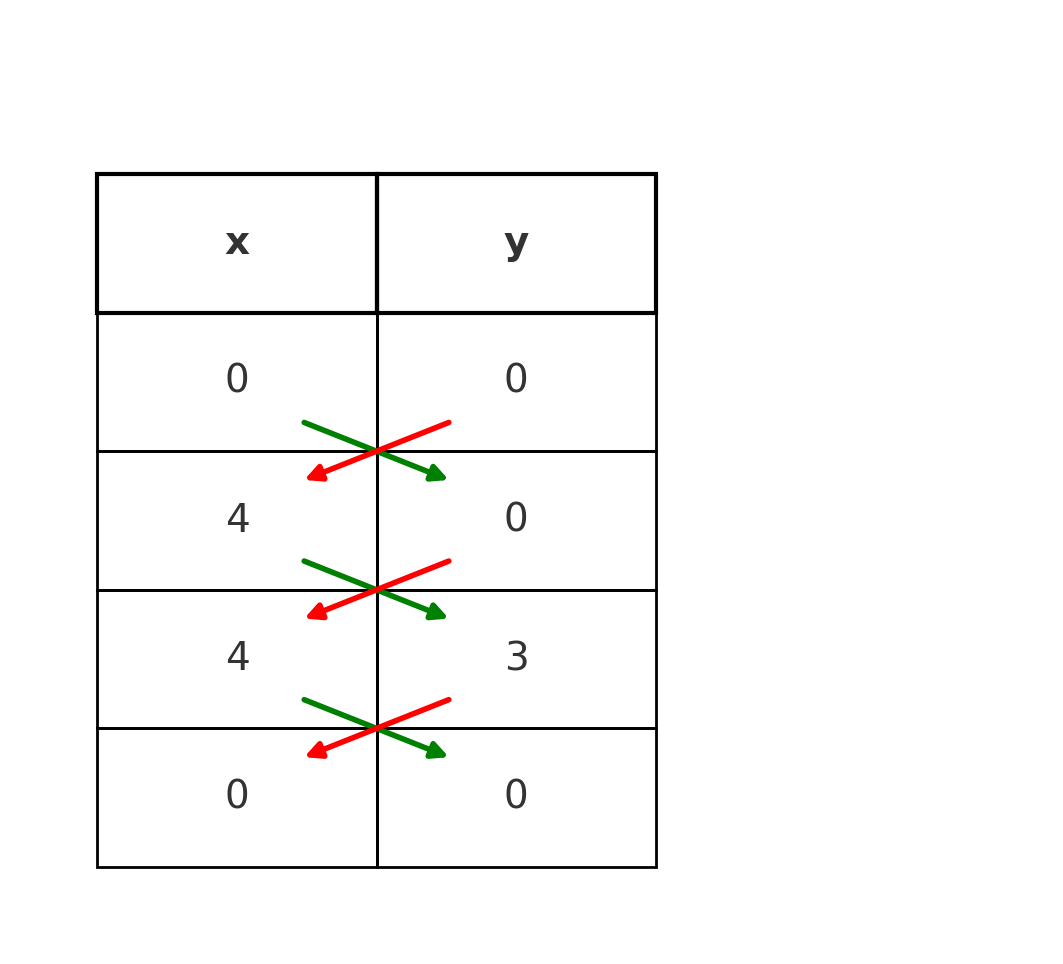
This image shows why the method is called the shoelace formula.

First, arrows are drawn from left to right for the products that are added. Then, arrows are drawn from right to left for the products that are subtracted.

The pattern of crossing arrows comes to resemble a shoelace.

 

 

Example 2: Quadrilateral

Find the area of the quadrilateral with points \( \large (0,0), (5,0), (6,2), (1,3) \).

 

Insert into the scheme:

 

$$ \large A = \frac{1}{2} \left| 0 \cdot 0 + 5 \cdot 2 + 6 \cdot 3 + 1 \cdot 0 - \big( 0 \cdot 5 + 0 \cdot 6 + 2 \cdot 1 + 3 \cdot 0 \big) \right| $$

$$ \large A = \frac{1}{2} \left( 28 - 2 \right) = \frac{1}{2} \cdot 26 = 13 $$

 

The area of the quadrilateral is 13.

 

 

Remarks

• The order (clockwise or counterclockwise) gives the same result because of the absolute value.
• The method requires a non-self-intersecting polygon.
• Complex figures can be divided into simple polygons, after which the areas are summed.