Polygons

A polygon is a "many-sided figure", that is, a figure with many sides.

So what does "many sides" mean?

It covers all figures with sides, including triangles and quadrilaterals. We have given them separate names instead of just saying "a polygon with three sides".

So polygon is a general term for figures with several sides.

Different polygons

Polygons can either be convex or concave and regular or irregular:

	Convex	Concave
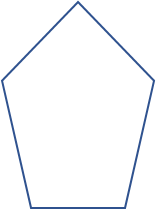
Regular	All angles are less than 180^o All sides are equal	One or more angles are greater than 180^o All sides are equal
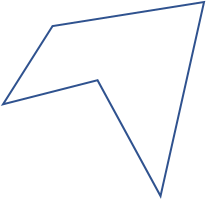
Irregular	All angles are less than 180^o Sides are not equal	One or more angles are greater than 180^o Sides are not equal

Figures

Here the four types are shown as figures:

	Convex	Concave
Regular
Irregular

Complex polygon

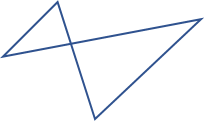
The four above are all called simple polygons, and in addition there are complex polygons where the lines also cross each other.

Complex polygon

Angle sum in polygons

The angle sum in a polygon can be calculated with the following formula:

$$ Angle\ sum = (Number\ of\ sides - 2) \cdot 180 \\[12pt] \Leftrightarrow \\[12pt] \sum \alpha = (n-2)\cdot 180 $$

If you use this formula on concave polygons, remember that it calculates the interior angle sum.

Area

For regular convex polygons there is a formula that can calculate the area:

$$ Area=\frac{1}{4} \cdot n \cdot b^2 \cdot cot \biggl( \frac{\pi}{n} \biggr) $$

Where $n$ = number of sides and $b$ = side length.

If you have a pentagon with a side length of 8, it would look like this:

$$ Area=\frac{1}{4} \cdot 5 \cdot 8^2 \cdot cot \biggl( \frac{\pi}{5} \biggr) \Leftrightarrow $$

$$ Area=\frac{5 \cdot 64 \cdot 1.376382}{4} \Leftrightarrow $$

$$ Area = 110.11 $$

Cot is cotangent (cosine divided by sine). If your calculator does not have that button, you can calculate it like this:

$$ cot \biggl( \frac{\pi}{n} \biggr)= \frac{cos \biggl( \frac{\pi}{n} \biggr)}{sin \biggl( \frac{\pi}{n} \biggr)} $$

Perimeter

There are no special rules for the perimeter. You just need to find the side lengths and add them together.

In general, when calculating polygons and no formula exists, the task is to divide the figure into shapes you can calculate.

Here it is useful to have an overview of trigonometry.

Pentagram

A well-known complex polygon that most people can easily draw is a pentagram.

It can be drawn in one stroke without lifting the pencil.

Pentagram

The pentagram is a complex polygon because the lines cross each other.

The pentagram shown is also regular because all sides are equal in length.

Decagon (Ten-sided polygon)

The decagon below is not a complex polygon. It is a concave regular polygon.

Decagon

It could also be drawn irregularly. The interior angle sum of the ten-sided polygon is 1440^o

Names of polygons

Number of sides	Name	Angle sum
3	Trigon	180^o
4	Tetragon	360^o
5	Pentagon	540^o
6	Hexagon	720^o
7	Heptagon	900^o
8	Octagon	1,080^o
9	Nonagon	1,260^o
10	Decagon	1,440^o
11	Hendecagon	1,620^o
12	Dodecagon	1,800^o
13	Tridecagon	1,980^o
14	Tetradecagon	2,160^o
15	Pentadecagon	2,340^o
16	Hexadecagon	2,520^o
17	Heptadecagon	2,700^o
18	Octadecagon	2,880^o
19	Enneadecagon	3,060^o
20	Icosagon	3,240^o
50	Pentacontagon	8,640^o
1,000	Chiliagon	179,640^o
10,000	Myriagon	1,799,640^o