Secant method

The secant method is a numerical technique for finding a root of a function, that is, a point where \( \large f(x) = 0 \). It resembles the Newton-Raphson method, but instead of using the derivative \( \large f'(x) \), the tangent is replaced by a secant through two points on the graph.

 

 

The idea behind the method

At each step, the two most recent points \( \large (x_{n-1}, f(x_{n-1})) \) and \( \large (x_n, f(x_n)) \) are used to form a straight line (secant). The intersection of this secant with the x-axis is used as the new estimate \( \large x_{n+1} \). The method is repeated until two successive estimates are very close.

 

 

Formula

 

$$ \large x_{n+1} = x_n - f(x_n) \cdot \frac{x_n - x_{n-1}}{f(x_n) - f(x_{n-1})} $$

 

 

Step-by-step procedure

 

1. Choose two starting values \( \large x_0 \) and \( \large x_1 \), where the function has opposite signs.
2. Compute \( \large f(x_0) \) and \( \large f(x_1) \).
3. Use the formula to find \( \large x_2 \).
4. Repeat the calculation so that \( \large x_{n+1} \) is found using the two most recent points \( \large x_n \) and \( \large x_{n-1} \).
5. Stop when \( \large |x_{n+1} - x_n| < \varepsilon \).

 

 

Example

We seek the root of \( \large f(x) = x^3 - x - 2 \).

 

Choose \( \large x_0 = 1 \) and \( \large x_1 = 2 \).

 

$$ \large f(1) = -2, \quad f(2) = 4 $$

 

$$ \large x_2 = 2 - 4 \cdot \frac{2 - 1}{4 - (-2)} $$

$$ \large x_2 = 2 - 4 \cdot \frac{1}{6} $$

$$ \large x_2 = 1{,}333 $$

 

The new point \( \large x_2 = 1{,}333 \) is used together with \( \large x_1 = 2 \) to calculate the next value:

 

$$ \large x_3 = 1{,}333 - f(1{,}333) \cdot \frac{1{,}333 - 2}{f(1{,}333) - f(2)} $$

 

After a few iterations, a root is obtained \( \large x \approx 1{,}521 \), the same result as with Newton-Raphson, but without knowing the derivative of the function.

 

 

 

 

 

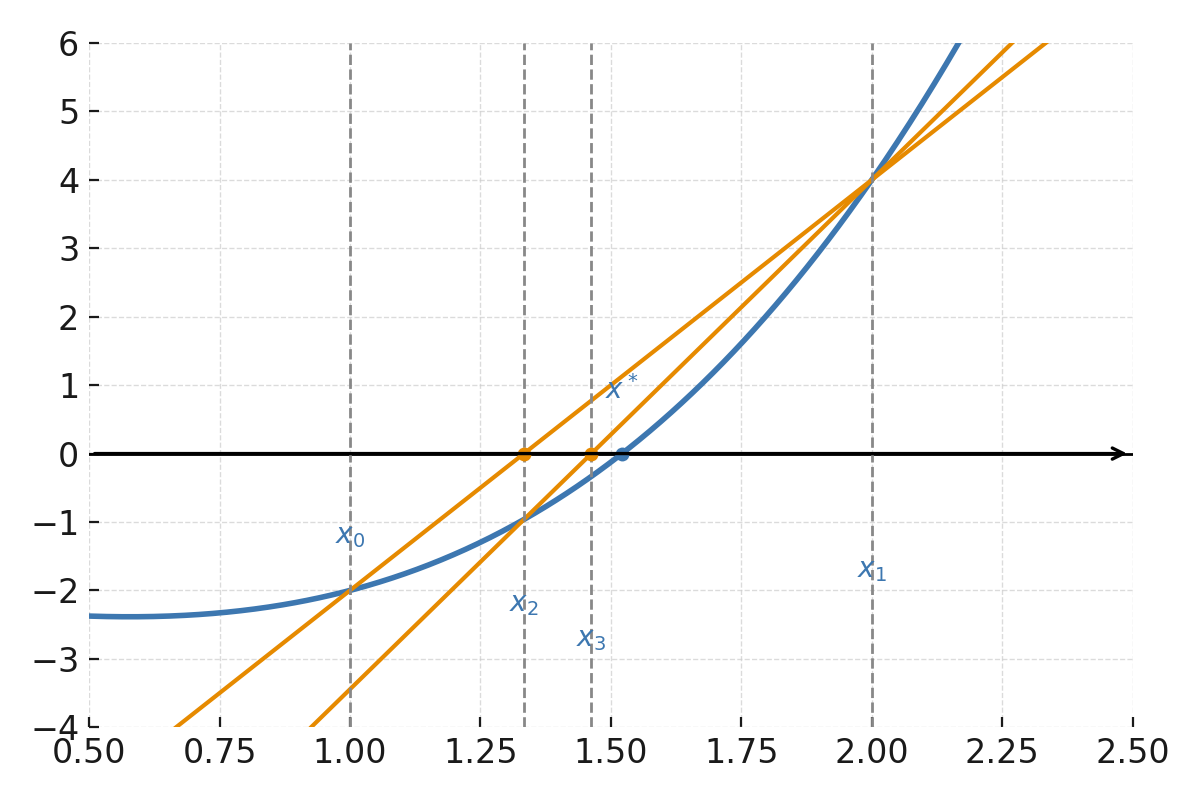
The function \( \large f(x) = x^3 - x - 2 \).

The points \( \large (x_0, f(x_0)) \) and \( \large (x_1, f(x_1)) \) are connected by a secant that intersects the x-axis at \( \large x_2 \). Then, a new secant is drawn between \( \large (x_1, f(x_1)) \) and \( \large (x_2, f(x_2)) \), which intersects the axis even closer to the root.

 

 

Remarks

The secant method converges faster than the bisection method but slower than Newton-Raphson. However, it is often a good compromise because it does not require calculating the derivative of the function.