Newton-Raphson method

The Newton-Raphson method is a fast numerical technique for finding roots of a function, that is, points where $ \large f(x) = 0 $. The method uses both the function value and its derivative to improve the estimate of the root’s position.

The idea behind the method

The starting point is an initial guess $ \large x_0 $. At the point $ \large (x_0, f(x_0)) $, the tangent to the curve is drawn. The intersection of this tangent with the x-axis is used as the new guess $ \large x_1 $. The process is repeated until the difference between two successive guesses is smaller than a chosen tolerance $ \large \varepsilon $.

Formula

$$ \large x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} $$

Step-by-step procedure

Choose a starting point $ \large x_0 $.
Calculate $ \large f(x_0) $ and $ \large f'(x_0) $.
Use the formula to find $ \large x_1 $.
Repeat until $ \large |x_{n+1} - x_n| < \varepsilon $.

Example

We want to find the root of $ \large f(x) = x^3 - x - 2 $, which we previously solved using the bisection method.

The derivative is $ \large f'(x) = 3x^2 - 1 $.

We choose an initial guess $ \large x_0 = 1{,}5 $.

$$ \large f(1{,}5) = (1{,}5)^3 - 1{,}5 - 2$$

$$ \large f(1{,}5) = -0{,}125 $$

$$ \large f'(1{,}5) = 3(1{,}5)^2 - 1 $$

$$ \large f'(1{,}5) = 5{,}75 $$

$$ \large x_1 = 1{,}5 - \frac{-0{,}125}{5{,}75} $$

$$ \large x_1 = 1{,}5217 $$

After a few iterations, the method quickly converges to the root $ \large x \approx 1{,}521 $.

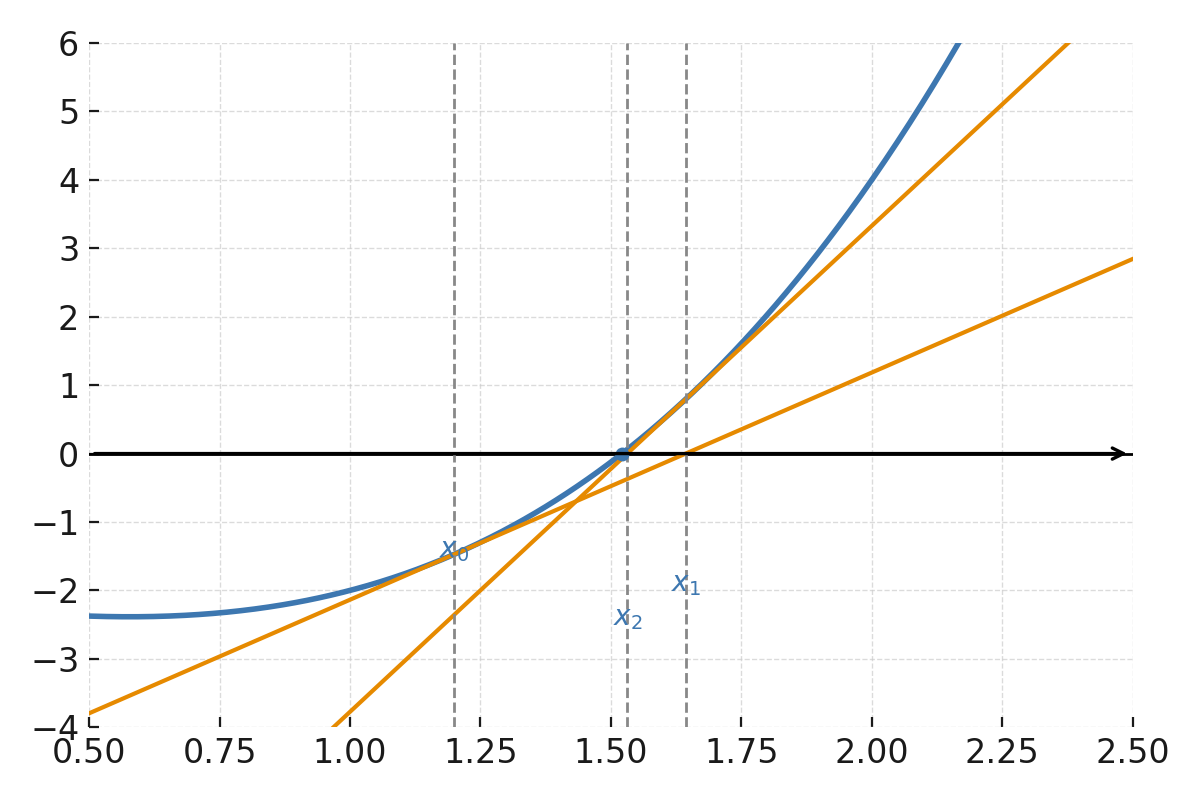
Newton-Raphson method

The function $ \large f(x) = x^3 - x - 2 $. The initial guess $ \large x_0 $ is marked on the x-axis, and the tangent at $ \large x_0 $ is drawn as a line intersecting the x-axis at $ \large x_1 $. Next, the tangent at $ \large x_1 $ is shown, intersecting even closer to the root. The figure illustrates the iterative improvement.

Remarks

The Newton-Raphson method converges much faster than the bisection method, but it requires that the derivative $ \large f'(x) $ can be computed and that the initial guess is close to the actual root. If the tangent is almost horizontal (that is, $ \large f'(x) \approx 0 $), the method may fail or overshoot the root.