Applications of integral calculus
Integrals are not only used to calculate areas but also in many different contexts where one needs to sum small contributions to a total quantity. In physics, economics, and geometry, integrals provide a precise mathematical tool to measure total growth, energy, mass, distance, or volume.
Area between two curves
One of the most common applications is finding the area between two functions \( \large f(x) \) and \( \large g(x) \). If \( \large f(x) \ge \large g(x) \) in the interval \([ \large a,\large b ]\), the area is calculated as the difference between the two:
$$ \large A \;=\; \int_a^b \big(f(x) - g(x)\big)\,dx $$
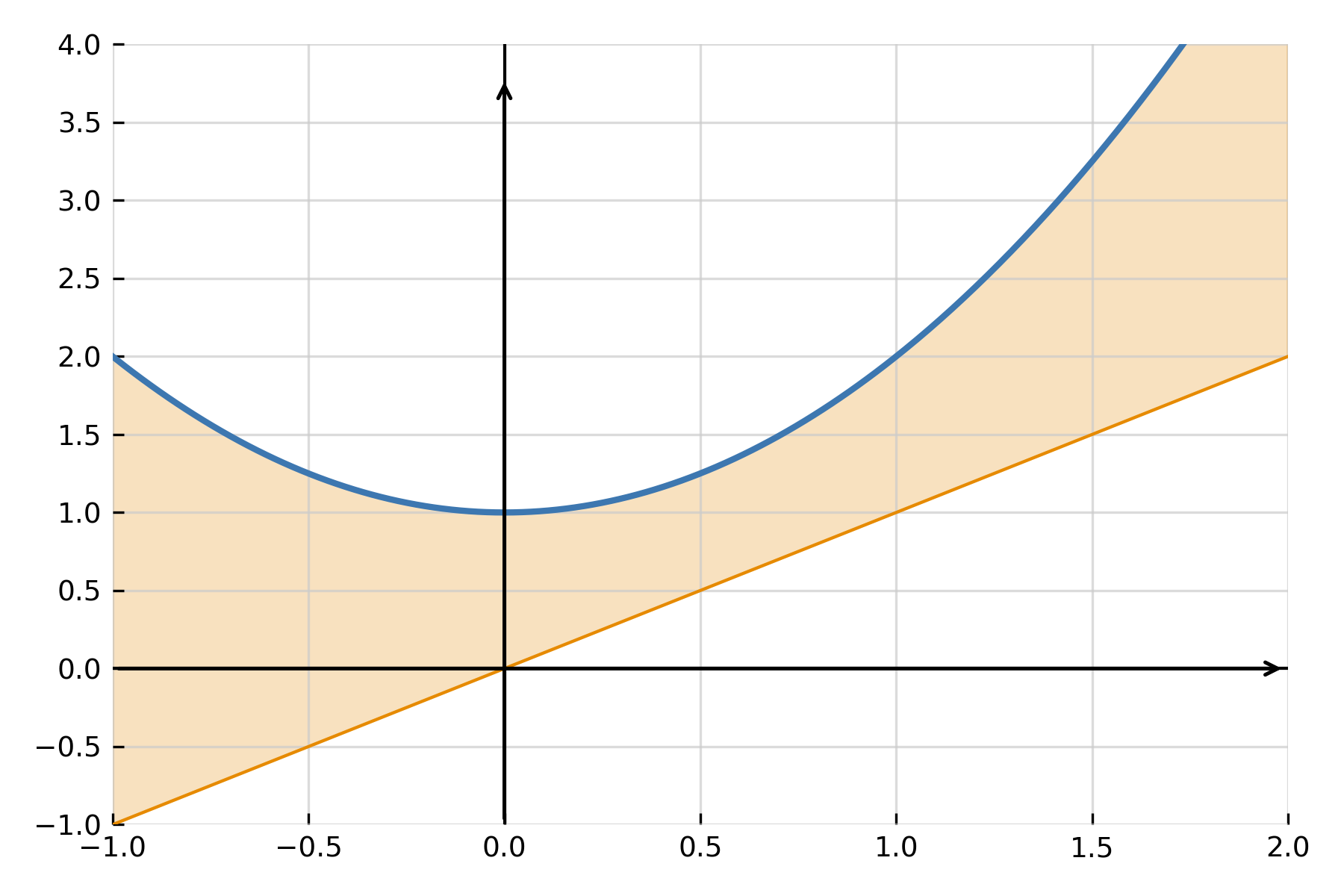
The integral precisely measures the vertical distance between the curves for each \( \large x \) and sums it over the interval. If the graphs intersect, the interval is divided into sections where the positive difference is taken each time.
Volume of solids of revolution
When a function is rotated around the x-axis, it forms a three-dimensional solid. The volume can be found by summing the cross-sectional areas (disks) along the axis:
$$ \large V \;=\; \pi \int_a^b \big(f(x)\big)^2\,dx $$
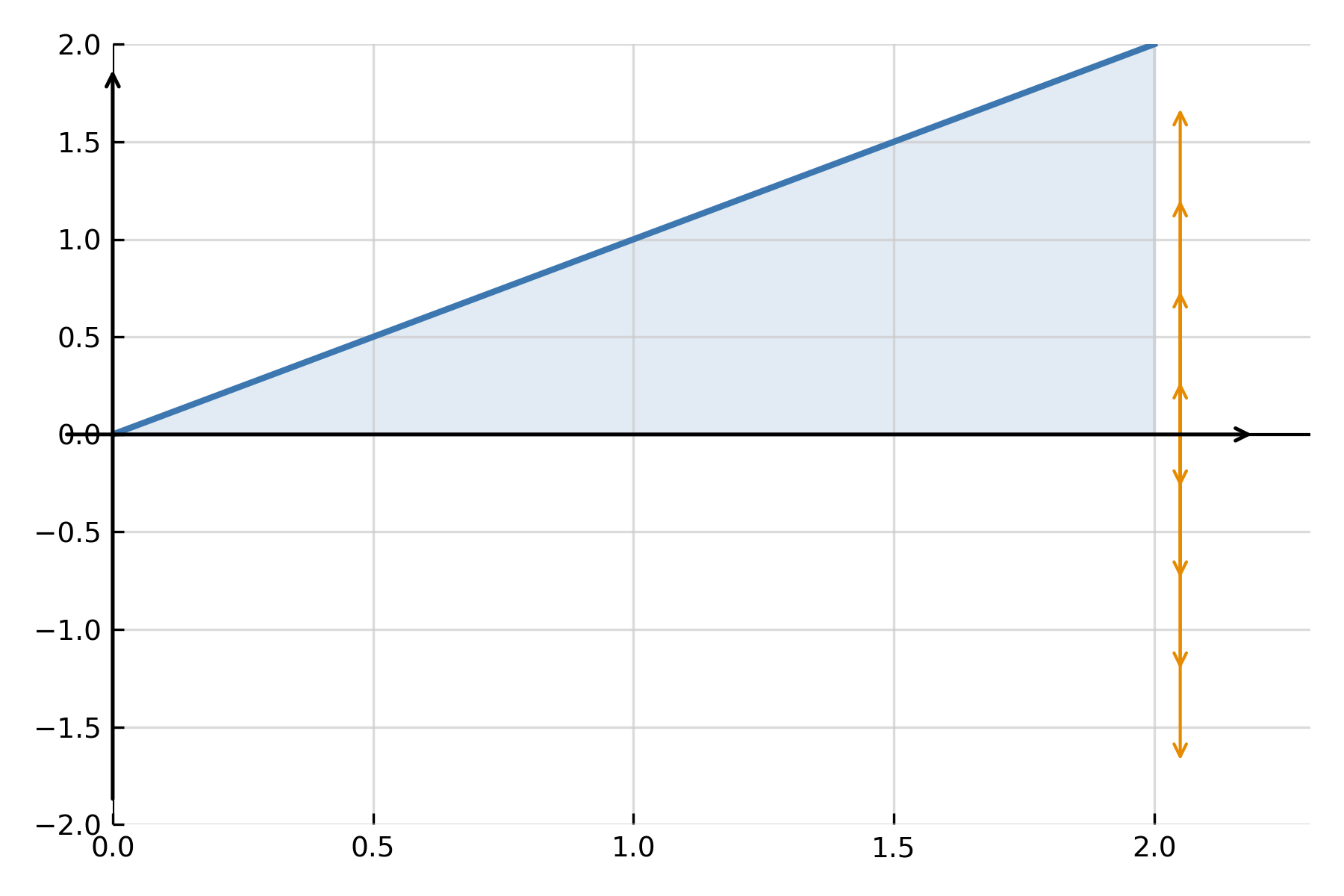
Here, \( \large f(x) \) is the radius of the rotated function at the point \( \large x \). The integral sums infinitely many small disks that together form the total volume.
Example: Solid of revolution
Find the volume of the solid formed by rotating \( \large f(x)=x \) around the x-axis from \( \large x=0 \) to \( \large x=2 \):
$$ \large V \;=\; \pi \int_0^2 x^2\,dx \;=\; \pi \Big[\tfrac{1}{3}x^3\Big]_0^2 \;=\; \tfrac{8}{3}\pi $$
This corresponds to the volume of a cone with height 2 and radius 2.
Work and energy
In physics, integrals are used to calculate work when a force varies with position. The work \( \large W \) is the sum of small force contributions \( \large F(x)\,dx \):
$$ \large W \;=\; \int_a^b F(x)\,dx $$
If the force is constant, this reduces to \( \large W = F \cdot s \), but the integral allows calculation when the force changes along the motion.
Motion and distance traveled
When the velocity function \( \large v(t) \) of an object is known, the integral of \( \large v(t) \) gives the distance traveled:
$$ \large s \;=\; \int_{t_1}^{t_2} v(t)\,dt $$
If the velocity can be negative (movement backward), one must integrate with sign. If the total distance regardless of direction is desired, use \( \large \int |v(t)|\,dt \) instead.
Economic and biological applications
Integrals are also used to calculate accumulated growth, consumption, or income over time. In economics, \( \large f(x) \) may represent a marginal function, for example revenue per unit, and the integral gives the total income. In biology, integrals are used to measure the total biomass, energy intake, or amount of substance of a population.
Average value of a function
The average value of a function over an interval is found by taking the total area and dividing by the length of the interval:
$$ \large f_{\text{avg}} \;=\; \frac{1}{b-a}\int_a^b f(x)\,dx $$
This formula is used in statistics, physics, and analysis to find mean values of continuous functions.
When an integral cannot be evaluated analytically, one can instead use numerical methods such as the rectangle rule, the trapezoidal rule, or Simpson’s rule to find an approximate value. These methods are described in the section Numerical methods.
Summary
Integrals are used to calculate areas, volumes, energy, work, and much more. What all applications have in common is that the integral sums small parts into a total quantity. Thus, integral calculus forms a central tool for describing and calculating relationships in nature, engineering, and economics.