Integral calculus

Integral calculus is about summing small contributions to obtain a total quantity. While differential calculus measures instantaneous changes (\( \large \text{slopes} \)), integral calculus measures accumulated quantities such as area, distance, total growth, or energy. The two branches are closely related: differentiation and integration are inverse processes.

 

 

What is integral calculus

When a quantity changes gradually, one can imagine dividing the process into many small parts and adding them together. This is the essence of integral calculus: the sum of “small pieces” becomes a global quantity. In practice, this is expressed through integrals.

 

 

Geometric interpretation

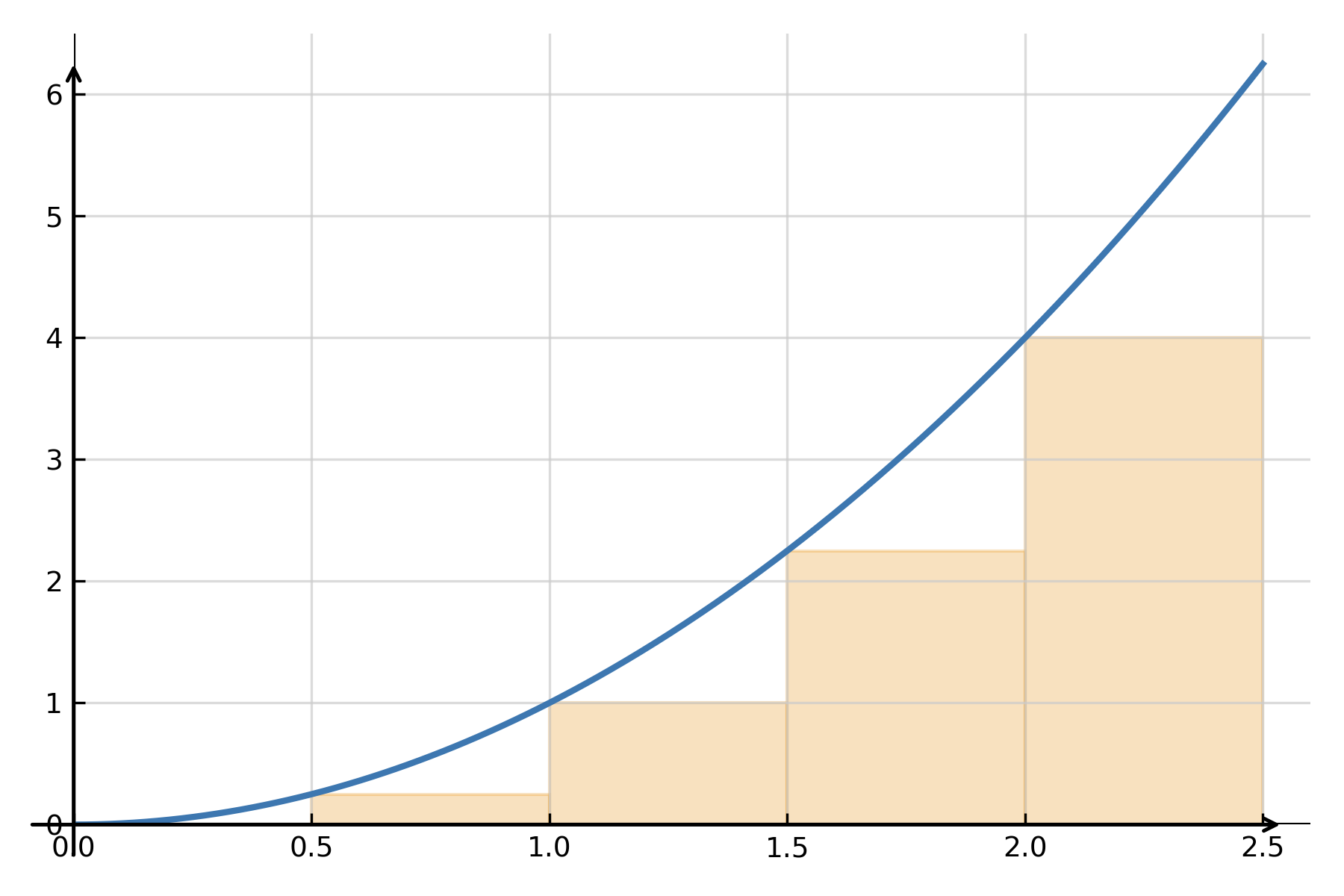
A classic interpretation is the area under the graph of a non-negative function \( \large f(x) \) between \( \large x=a \) and \( \large x=b \). The area can be approximated by dividing the interval into narrow rectangles, computing their areas, and adding them together. As the width approaches zero, the sum approaches the exact area.

 

$$ \large \text{Area} \;=\; \lim_{n \to \infty} \sum_{i=1}^{n} f(x_i)\,\Delta x \;=\; \int_a^b f(x)\,dx $$

 

The integral therefore provides a precise way to measure an “accumulated quantity,” whether it is area, mass, work, or something else.

 

 

 

Indefinite integral (antiderivative)

The indefinite integral represents “reverse differentiation.” If \( \large F'(x)=f(x) \), then \( \large F \) is called an antiderivative of \( \large f \), and we write:

 

$$ \large \int f(x)\,dx \;=\; F(x) + C $$

 

Here \( \large C \) is an arbitrary constant. The indefinite integral represents all functions that share the same derivative \( \large f \).

 

 

Definite integral (area and sum)

The definite integral measures the accumulated quantity between two limits \( \large a \) and \( \large b \). It is defined as the limit of Riemann sums:

 

$$ \large \int_a^b f(x)\,dx \;=\; \lim_{n\to\infty}\sum_{i=1}^{n} f(x_i)\,\Delta x $$

 

If \( \large f \ge 0 \) on the interval, this represents the area under the graph. If \( \large f \) changes sign, the area below the x-axis counts as negative, reflecting the net accumulation.

 

 

Connection to differential calculus (Fundamental Theorem)

Integral and differential calculus are linked by the fundamental theorem: If \( \large f \) is continuous on \( \large [a,b] \) and \( \large F \) is an antiderivative of \( \large f \), then

 

$$ \large \int_a^b f(x)\,dx \;=\; F(b) - F(a) $$

 

This means that an area (a sum) can be found using an antiderivative, and that differentiation and integration are inverse processes.

 

 

Examples

1. Area under a simple function

Find \( \large \int_0^2 x\,dx \). An antiderivative is \( \large F(x)=\tfrac{1}{2}x^2 \), so

 

$$ \large \int_0^2 x\,dx \;=\; \Big[\tfrac{1}{2}x^2\Big]_0^2 \;=\; \tfrac{1}{2}\cdot 4 - 0 \;=\; 2 $$

 

2. Accumulated distance from a velocity function

If a car’s velocity is \( \large v(t)=3t \) (m/s), then the distance traveled from \( \large t=0 \) to \( \large t=4 \) is:

 

$$ \large s \;=\; \int_0^4 v(t)\,dt \;=\; \int_0^4 3t\,dt \;=\; \Big[\tfrac{3}{2}t^2\Big]_0^4 \;=\; 24\ \text{m} $$

 

This shows that the area under the velocity curve equals the total distance traveled.

 

 

Why two types of integrals

The indefinite integral (antiderivative) is a tool for finding formulas and working algebraically, while the definite integral \( \large \text{measures} \) a concrete quantity over an interval. The fundamental theorem allows us to translate between these two perspectives.

 

 

Summary

Integral calculus is about summing small contributions to form a total quantity. Geometrically, integrals are interpreted as areas; physically, as accumulated mass, work, or distance. Through the fundamental theorem, definite integrals can be computed via antiderivatives, making integral calculus the natural “inverse” process of differentiation.