The derivative function

The derivative function describes how fast another function changes. If \( \large f(x) \) represents a quantity, the derivative \( \large f'(x) \) indicates how much that quantity changes when \( \large x \) changes slightly. In this way, differential calculus becomes a precise tool for measuring change.

 

 

From secant to tangent

To understand what it means to “differentiate,” one begins with the slope of a secant. A secant is the straight line connecting two points on the graph of \( \large f(x) \). The slope of the secant shows how much the function increases or decreases on average between the two points.

 

$$ \large a_{\text{secant}} = \frac{f(x+h) - f(x)}{h} $$

 

If the points are chosen closer and closer together so that \( \large h \) becomes very small, the secant approaches a line that touches the graph at only one point — the tangent line. The slope of this tangent is called the instantaneous rate of change. This is precisely the value given by the derivative function.

 

 

 

 

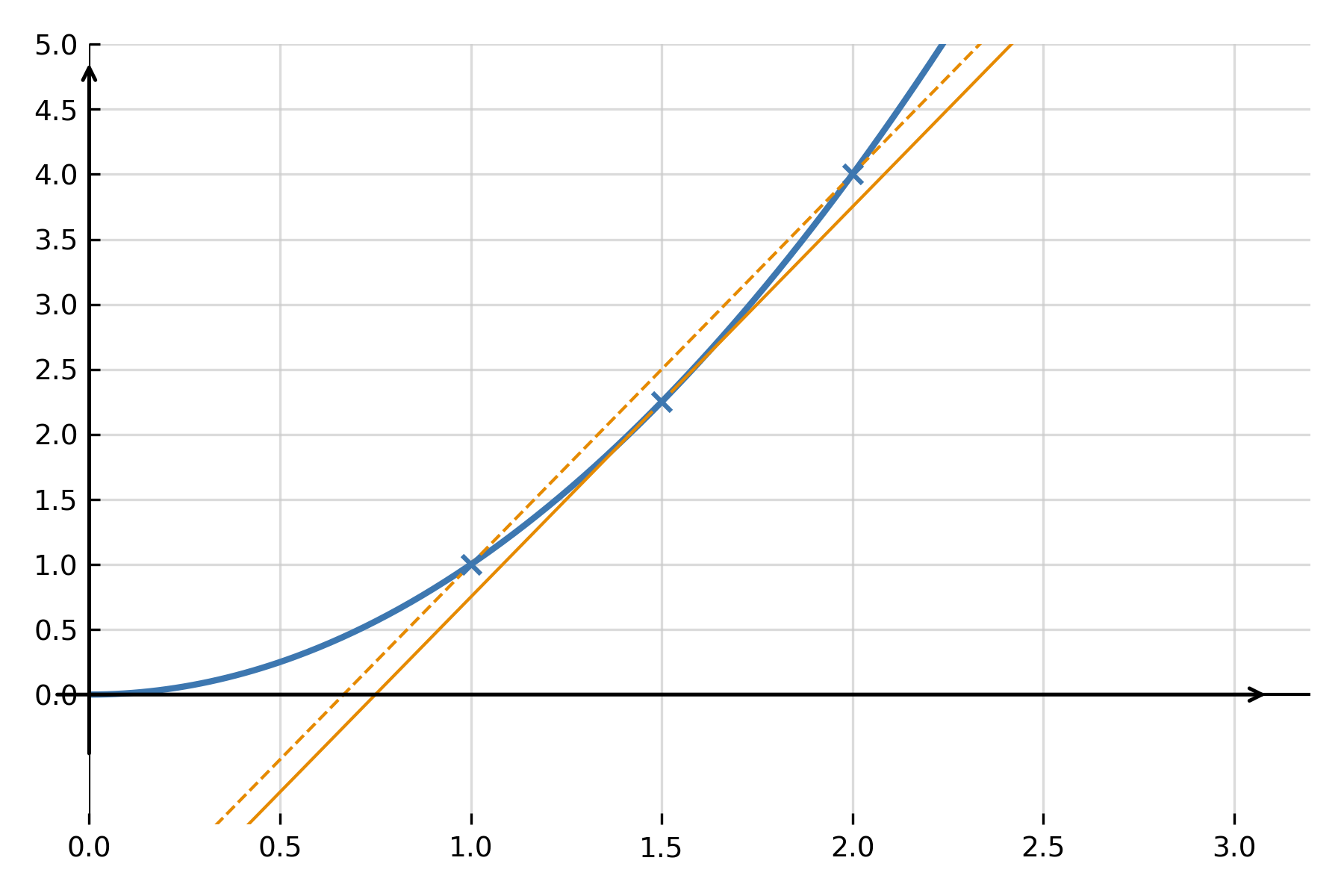
Definition via limit

The precise definition of the derivative function is:

 

$$ \large f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} $$

 

Here, the fraction measures how much \( \large f(x) \) changes when \( \large x \) changes by a small amount \( \large h \). As \( \large h \) approaches zero, we obtain the rate of change at exactly that point — the slope of the tangent. The limit exists only if the function is smooth enough at that point, meaning there are no jumps, cusps, or corners.

 

 

Notation and reading

There are several ways to write the derivative:

 

$$ \large f'(x) \quad \text{or} \quad \frac{dy}{dx} \quad \text{or} \quad Df(x) $$

 

All three mean the same: how much \( \large y \) changes when \( \large x \) changes. In physics, for example, \( \large \frac{dy}{dt} \) is read as “change in distance over change in time,” that is, velocity.

 

 

Graphical understanding

The derivative function gives a new function that shows, at each point, the slope of the graph of \( \large f(x) \). Where the graph rises, the derivative is positive; where it falls, the derivative is negative; and where the graph has a horizontal tangent, the derivative is zero.

 

A point where \( \large f'(x) = 0 \) is called a stationary point. Such points play an important role later when finding maxima and minima of functions.

 

 

Physical interpretation

In many contexts, the derivative represents a physical quantity. If \( \large f(x) \) describes a position as a function of time, then \( \large f'(x) \) is the velocity — how fast the position changes. Differentiating once more gives the acceleration \( \large f''(x) \), which shows how quickly the velocity itself changes.

 

 

Examples

1. Example – quadratic function

For \( \large f(x) = x^2 \), the derivative can be computed directly from the definition:

 

$$ \large f'(x) = \lim_{h \to 0} \frac{(x+h)^2 - x^2}{h} = \lim_{h \to 0} \frac{2xh + h^2}{h} = 2x $$

 

The derivative function is \( \large f'(x) = 2x \). The slope therefore depends on where you are on the graph. At \( \large x = 3 \), the slope is \( \large f'(3) = 6 \).

 

2. Example – linear function

For \( \large f(x) = 5x + 2 \), the graph is already a straight line. Its slope is constant, so the derivative is:

 

$$ \large f'(x) = 5 $$

 

Here, the function always increases by 5 units when \( \large x \) increases by 1. This shows that differential calculus generalizes the familiar slope idea from straight lines to all smooth functions.

 

3. Example – physical interpretation

If \( \large s(t) = t^2 \) describes a car’s distance traveled in meters as a function of time \( \large t \) in seconds, then the velocity is \( \large v(t) = s'(t) = 2t \). After 4 seconds, the car’s speed is \( \large v(4) = 8 \) m/s. The derivative thus provides a direct measure of the rate of motion.

 

 

Mini rules

When finding derivatives of common functions, a few simple rules apply:

 

$$ \large (k)' = 0 \qquad (x^n)' = n \cdot x^{n-1} \qquad (k \cdot f(x))' = k \cdot f'(x) $$

 

These form the foundation for the general differentiation rules discussed in the next section. Using them, one can differentiate even quite complex functions without returning to the limit definition.

 

 

Summary

The derivative function expresses how fast a function changes at each point. It can be understood as the slope of the tangent line, as a measure of rate of change, or as a mathematical tool for describing motion and growth. It plays a central role in nearly all areas of mathematics, physics, and economics.