Applications of differential calculus

Differential calculus is not only used to calculate slopes. It also provides a deeper understanding of how functions behave. By studying the derivative, one can determine where a function increases or decreases, find its maximum and minimum, and analyze its graphical shape. The method is applied in everything from physics and economics to biology and engineering.

Monotonicity – where the function increases and decreases

The derivative function $ \large f'(x) $ shows whether $ \large f(x) $ is increasing or decreasing in a given interval:

If $ \large f'(x) > 0 $, the function is increasing.
If $ \large f'(x) < 0 $, the function is decreasing.
If $ \large f'(x) = 0 $, the function has a stationary point.

A stationary point is a place where the slope of the tangent is zero. It can be a local maximum, a local minimum, or an inflection point.

Example: Analyzing a function

Examine the function $ \large f(x) = x^3 - 3x^2 + 2 $.

First, find the derivative:

$$ \large f'(x) = 3x^2 - 6x = 3x(x - 2) $$

The derivative is zero for $ \large x = 0 $ and $ \large x = 2 $. We analyze the sign of $ \large f'(x) $ in the intervals:

For $ \large x < 0 $: $ \large f'(x) > 0 $ → increasing
For $ \large 0 < x < 2 $: $ \large f'(x) < 0 $ → decreasing
For $ \large x > 2 $: $ \large f'(x) > 0 $ → increasing

Thus, the function has a local maximum at $ \large x = 0 $ and a local minimum at $ \large x = 2 $. This method is called a sign chart and is used to determine where the function grows or decreases.

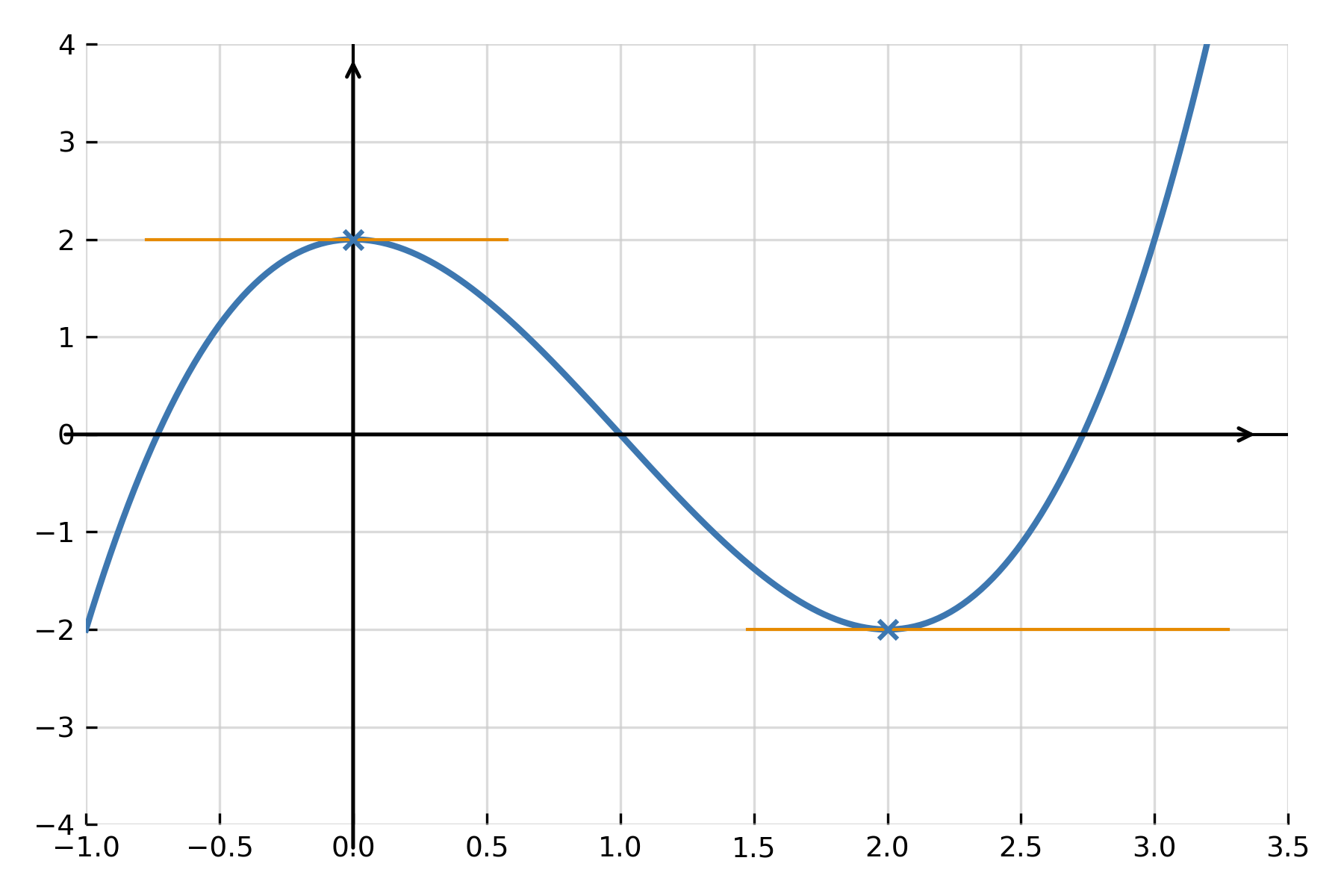
Extremum

Extrema, maximum and minimum

An extremum is a point where the function goes from increasing to decreasing (maximum) or from decreasing to increasing (minimum). To determine the type, one examines the sign of $ \large f'(x) $ around the point — or uses the second derivative.

The second derivative test states:

If $ \large f'(x_0) = 0 $ and $ \large f''(x_0) > 0 $, the function has a local minimum at $ \large x_0 $.
If $ \large f'(x_0) = 0 $ and $ \large f''(x_0) < 0 $, the function has a local maximum at $ \large x_0 $.

Example: For $ \large f(x) = x^3 - 3x^2 + 2 $, we have $ \large f''(x) = 6x - 6 $. Here $ \large f''(0) = -6 < 0 $ (maximum) and $ \large f''(2) = 6 > 0 $ (minimum).

Inflection points

An inflection point is a place where the curvature of the graph changes sign. This means the graph changes from being “concave up” to “concave down” or vice versa. An inflection point occurs where $ \large f''(x) = 0 $ and the sign changes.

Example: For $ \large f(x) = x^3 - 3x^2 + 2 $, $ \large f''(x) = 6x - 6 $, which becomes zero at $ \large x = 1 $. Since the sign changes here, the function has an inflection point at $ \large x = 1 $.

Optimization

Differential calculus is often used to solve optimization problems — that is, to find the largest or smallest value of a function under given conditions. This can, for example, mean maximizing an area, minimizing a cost, or finding the fastest path.

Step-by-step procedure:

Write down the function to be optimized.
Find its derivative $ \large f'(x) $.
Find the points where $ \large f'(x) = 0 $ (stationary points).
Use the sign or the second derivative to determine whether it is a maximum or a minimum.

Example – optimization

A rectangle has an area depending on its length $ \large x $:

$$ \large A(x) = x(12 - 2x) = 12x - 2x^2 $$

To find the largest area, differentiate the function:

$$ \large A'(x) = 12 - 4x $$

Set $ \large A'(x) = 0 $ → $ \large 12 - 4x = 0 \Rightarrow x = 3 $.

The second derivative $ \large A''(x) = -4 $ is negative, so this is a maximum. The rectangle therefore has its largest area when the length is $ \large 3 $ and the width is $ \large 12 - 2x = 6 $.

Graph sketch and interpretation

By combining information from $ \large f'(x) $ and $ \large f''(x) $, one can draw an accurate graph without using a calculator:

$ \large f'(x) $ shows where the graph rises or falls.
$ \large f''(x) $ shows whether the graph is concave up or concave down.
$ \large f'(x) = 0 $ gives peaks and troughs.
$ \large f''(x) = 0 $ gives inflection points.

This is called a complete graph analysis and forms the foundation for both theoretical understanding and practical applications of functions in science and technology.

Summary

The derivative makes it possible to analyze and predict how a function behaves. With differential calculus, one can find maxima and minima, determine intervals where the function increases or decreases, study the graph’s shape, and solve optimization problems. This makes it one of the most useful tools in all of mathematics.