Varians og standardafvigelse
Spredning
Spredning fortæller, hvor meget observationerne varierer omkring middelværdien.
Hvis alle observationer ligger tæt på middelværdien, er spredningen lille. Hvis de ligger langt fra middelværdien, er spredningen stor.
Varians
Variansen måler den gennemsnitlige kvadrerede afstand fra middelværdien.
For at finde variansen skal man:
- Trække middelværdien fra hver observation
- Kvadrere differencerne
- Find gennemsnittet af de kvadrerede differencer
$$ s^2 = \frac{(x_1 - \overline{x})^2 + (x_2 - \overline{x})^2 + ... + (x_n - \overline{x})^2}{n} $$
Standardafvigelse
Standardafvigelsen er kvadratroden af variansen. Den fortæller i samme enhed som observationerne, hvor meget de typisk afviger fra middelværdien.
$$ s = \sqrt{s^2} $$
Eksempel
Vi bruger observationen af elevernes højder.
- Middelværdien er \( \overline{x} = 164{,}8 \)
- Variansen er \( s^2 = 40{,}36 \)
- Standardafvigelsen er \( s \approx 6{,}35 \)
Det betyder, at højderne i gennemsnit afviger ca. 6,35 cm fra middelværdien.
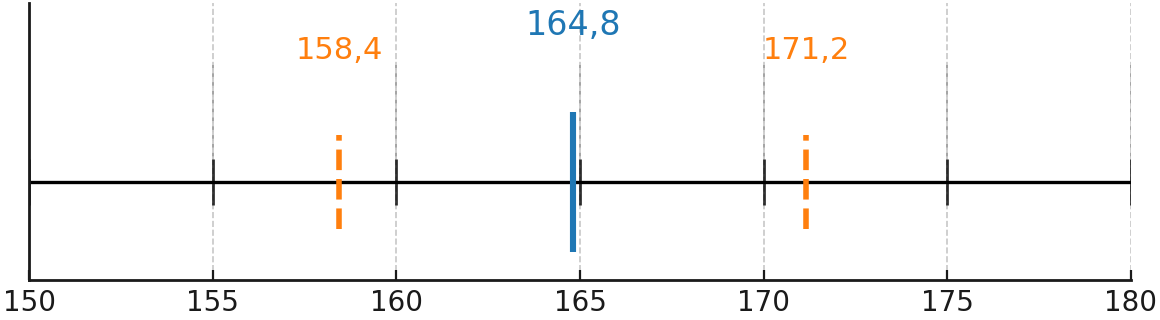
Diagram
Standardafvigelse kan vises i et diagram, hvor man markerer middelværdien og viser intervallerne \( \overline{x} \pm s \).