Secans og cosecans
Der findes også to reciprokke funktioner, nemlig secans og cosecans. De defineres som de omvendte værdier af cosinus og sinus:
$$ \large \sec(v) = \tfrac{1}{\cos(v)} \qquad \csc(v) = \tfrac{1}{\sin(v)} $$
Det betyder, at hvis du kender cosinus eller sinus til en vinkel, kan du finde secans eller cosecans ved blot at tage den reciprokke værdi.
For eksempel, hvis vinklen er 25°:
$$ \large \cos(25^\circ) \approx 0.906 \quad \Rightarrow \quad \sec(25^\circ) \approx 1.103 $$
$$ \large \sin(25^\circ) \approx 0.423 \quad \Rightarrow \quad \csc(25^\circ) \approx 2.366 $$
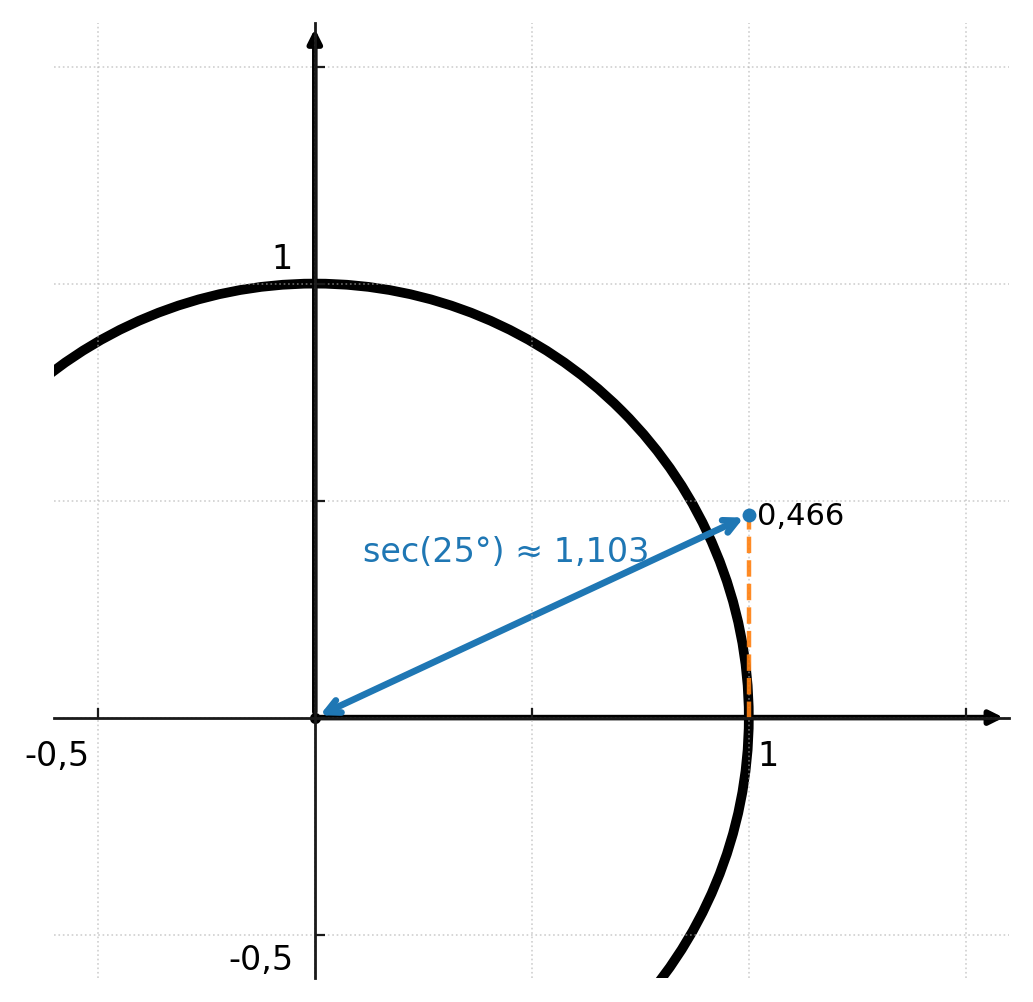
I enhedscirklen kan secans og cosecans også illustreres grafisk.
Begge funktioner findes ved at forlænge vinkelstrålen indtil den rammer henholdsvis linjen x = 1 (for secans) og linjen y = 1 (for cosecans).
Afstanden fra centrum til skæringspunktet er værdien af funktionen. Det ses på billedet herunder at tangens er 0,466 og secans er 1,103.
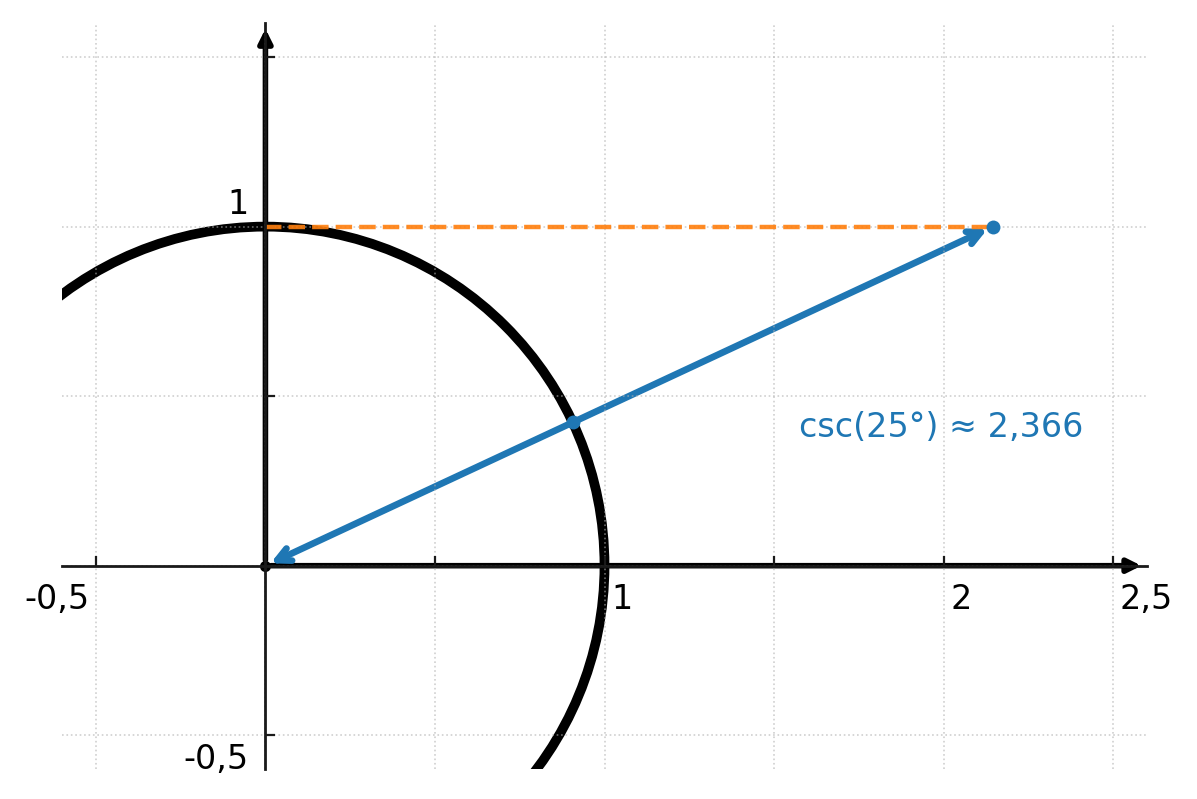
Her ses cosecans i enhedscirklen for vinklen på 25 grader, hvor længden fra centrum til skæringspunktet er 2.366
Anvendelse
Secans og cosecans er mest nyttige i f.eks. differentialregning og i andre avancerede områder af matematikken, hvor de gør visse beregninger enklere.
I almindelig geometri nøjes man som regel med sinus, cosinus og tangens.
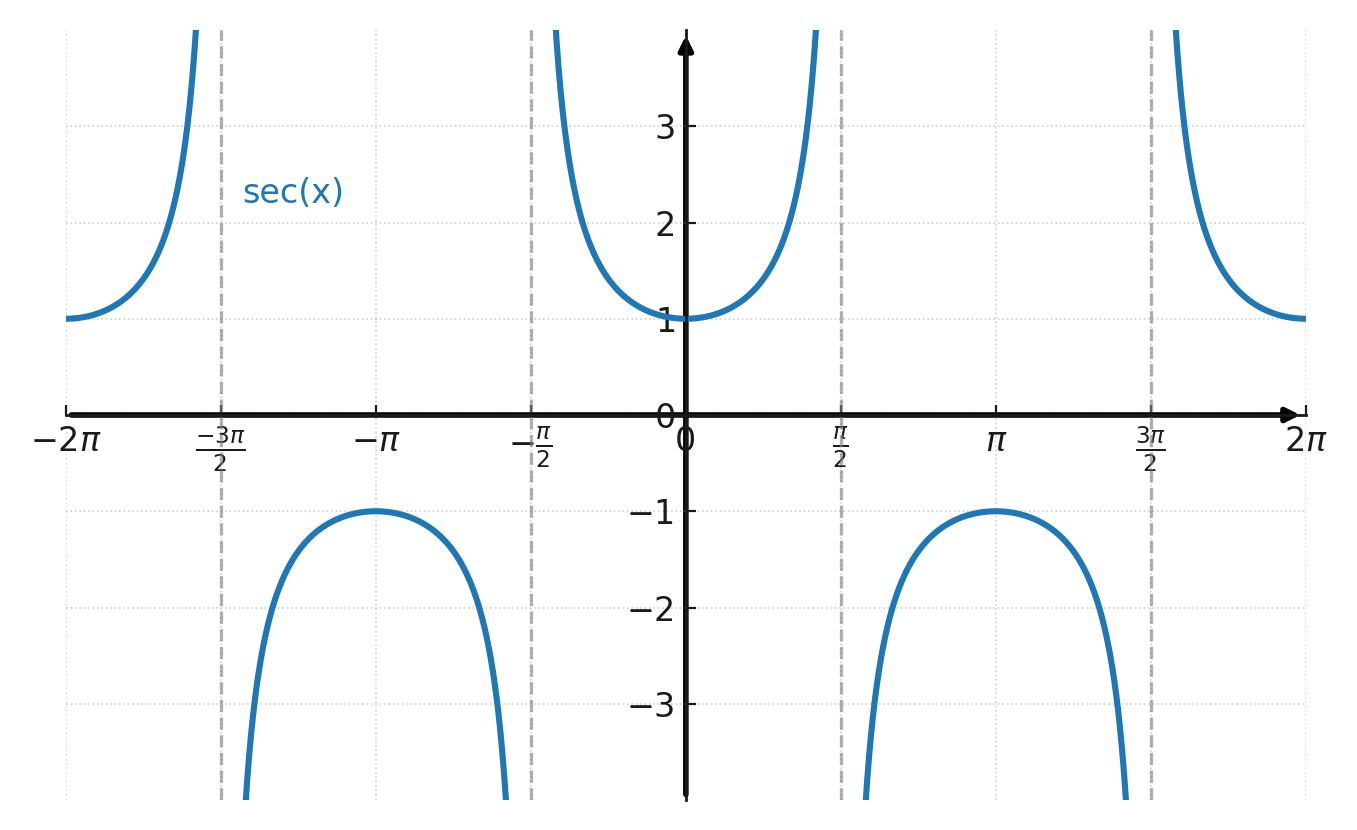
En hurtig blik på graferne for secans og cosecans forklarer hvorfor. Funktionerne har lodrette asymptoter, springer til meget store værdier og er ikke defineret alle steder, som sinus og cosinus er.
Graf for secans:
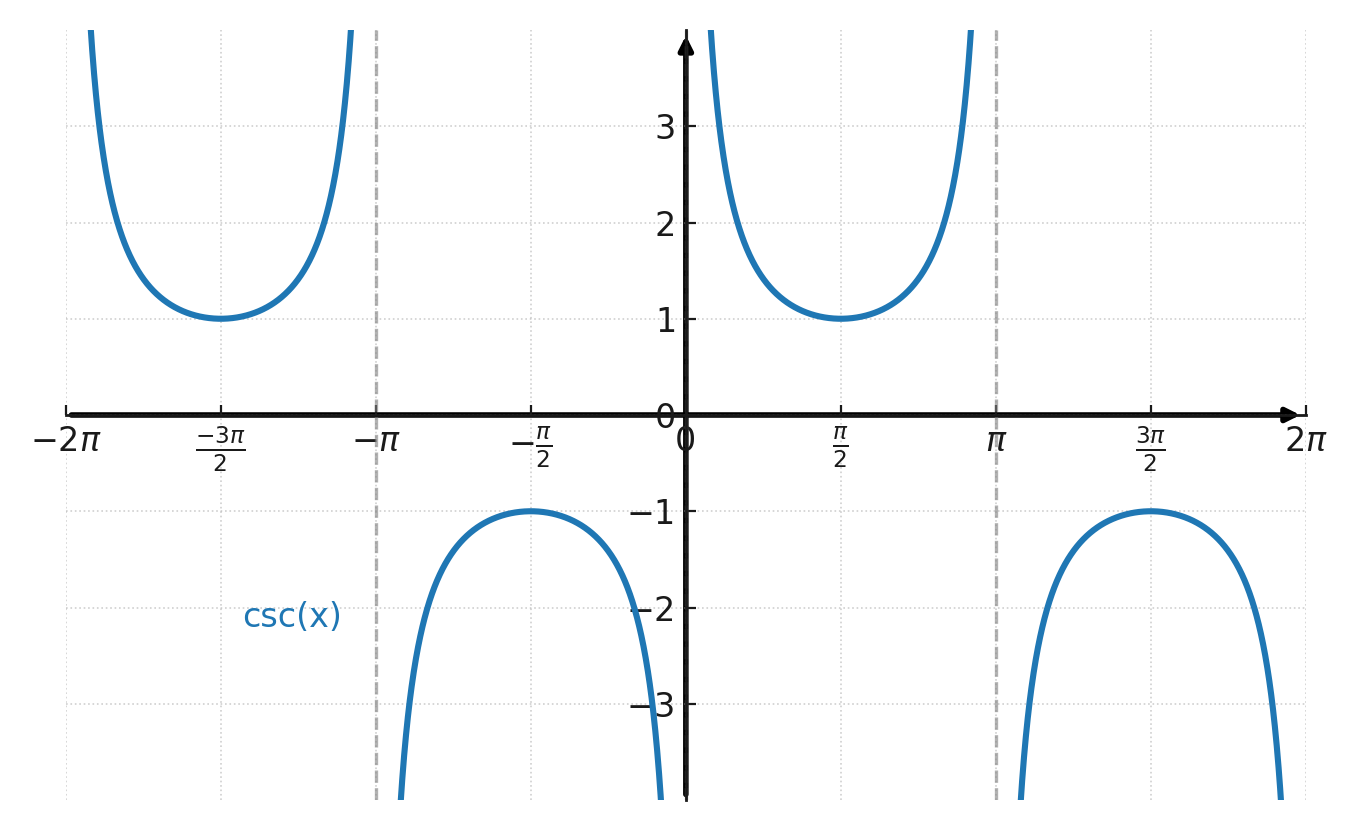
Graf for cosecans: