Relationer

I trigonometri handler relationer om de formler og sammenhænge, der binder de trigonometriske funktioner sammen. Hvor funktionerne (sinus, cosinus, tangens osv.) hver især beskriver et bestemt forhold, viser relationerne hvordan funktionerne hænger sammen og kan bruges til at beregne sider og vinkler i trekanter.

 

Pythagoras-identiteten

En af de mest grundlæggende relationer er Pythagoras-identiteten, som viser sammenhængen mellem sinus og cosinus for en vilkårlig vinkel:

 

$$ \sin^2(v) + \cos^2(v) = 1 $$

 

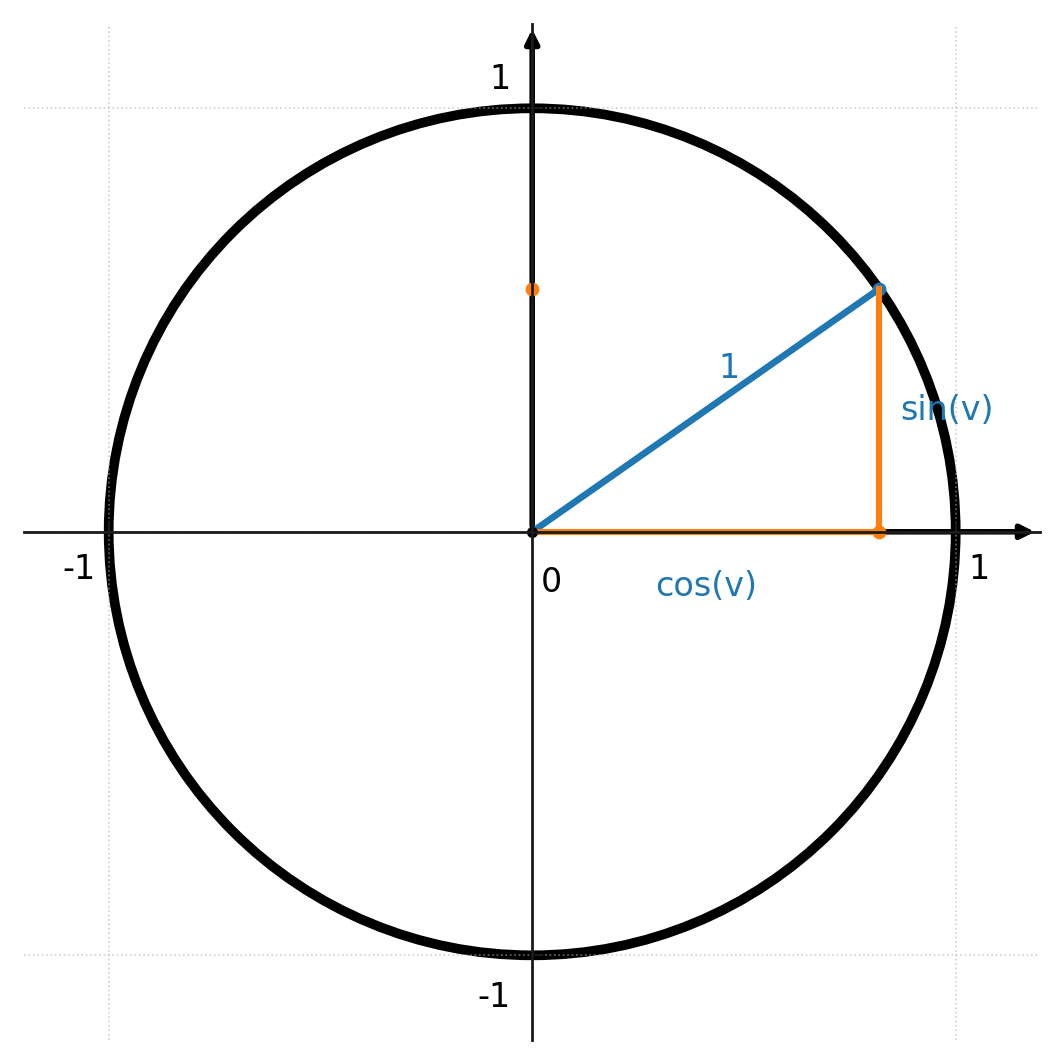
Identiteten følger direkte af enhedscirklen.

Hvis et punkt på cirklen har koordinaterne \( (\cos v, \sin v) \), gælder Pythagoras’ læresætning, fordi radius altid er 1:

 

$$ (\cos v)^2 + (\sin v)^2 = 1^2 = 1 $$

 

 

Anvendelse

Pythagoras-identiteten gør det muligt at beregne sinus, hvis man kender cosinus, eller cosinus, hvis man kender sinus.

Det er også grundlaget for mange andre trigonometriske identiteter.

 

Eksempel: Hvis \( \cos v = 0.6 \), kan sinus findes ved:

 

$$ \sin^2(v) = 1 - \cos^2(v) = 1 - 0.6^2 = 0.64 $$

$$ \sin(v) = \pm \sqrt{0.64} = \pm 0.8 $$

 

Bemærk at der er to løsninger, fordi vinklen kan ligge både i første og anden kvadrant.

 

Pythagoras-identiteten er den mest grundlæggende trigonometriske relation og danner udgangspunkt for mange andre formler og beregninger i trigonometri.