Dobbelt- og halvvinkelformler

I trigonometri beskriver dobbelt og halvvinkelformler hvordan sinus, cosinus og tangens kan udtrykkes, når vinklen fordobles eller halveres.

Formlerne bygger direkte på addition- og subtraktionsformlerne og gør det muligt at finde nye sammenhænge mellem de trigonometriske funktioner.

Ved at sætte $ \alpha = \beta $ i additionformlerne får vi:

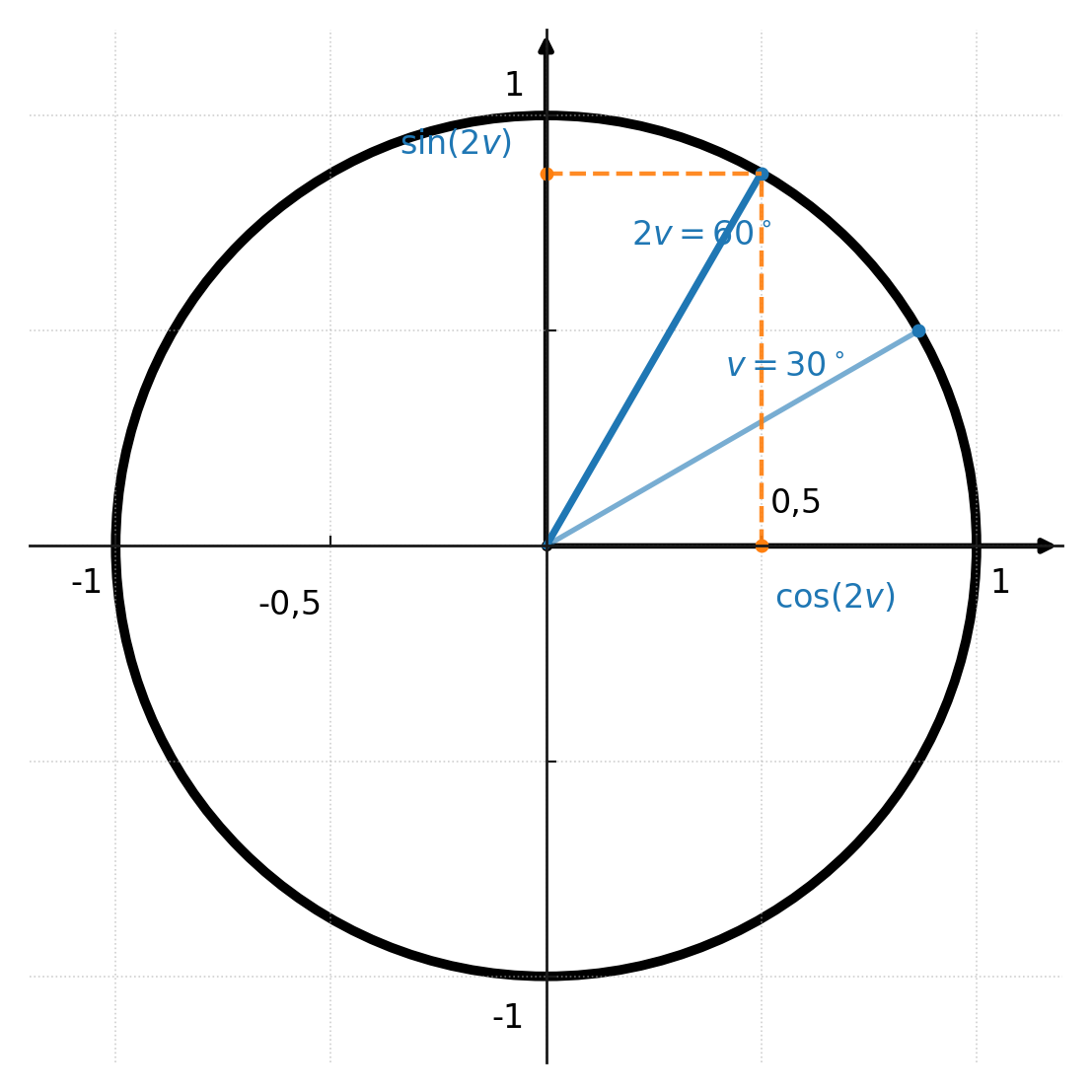
$$ \large \sin(2v) = 2 \sin(v) \cdot \cos(v) $$

$$ \large \cos(2v) = \cos^2(v) - \sin^2(v) $$

$$ \large \tan(2v) = \frac{2 \tan(v)}{1 - \tan^2(v)} $$

Trigonometriske relationer dobbeltvinkel

Cosinusformlen kan også omskrives til andre nyttige former ved hjælp af Pythagoras-identiteten:

$$ \large \cos(2v) = 2\cos^2(v) - 1 = 1 - 2\sin^2(v) $$

Halvvinkelformlerne fås ved at isolere $\sin v$ og $\cos v$ i dobbeltvinkelformlerne. Resultatet bliver:

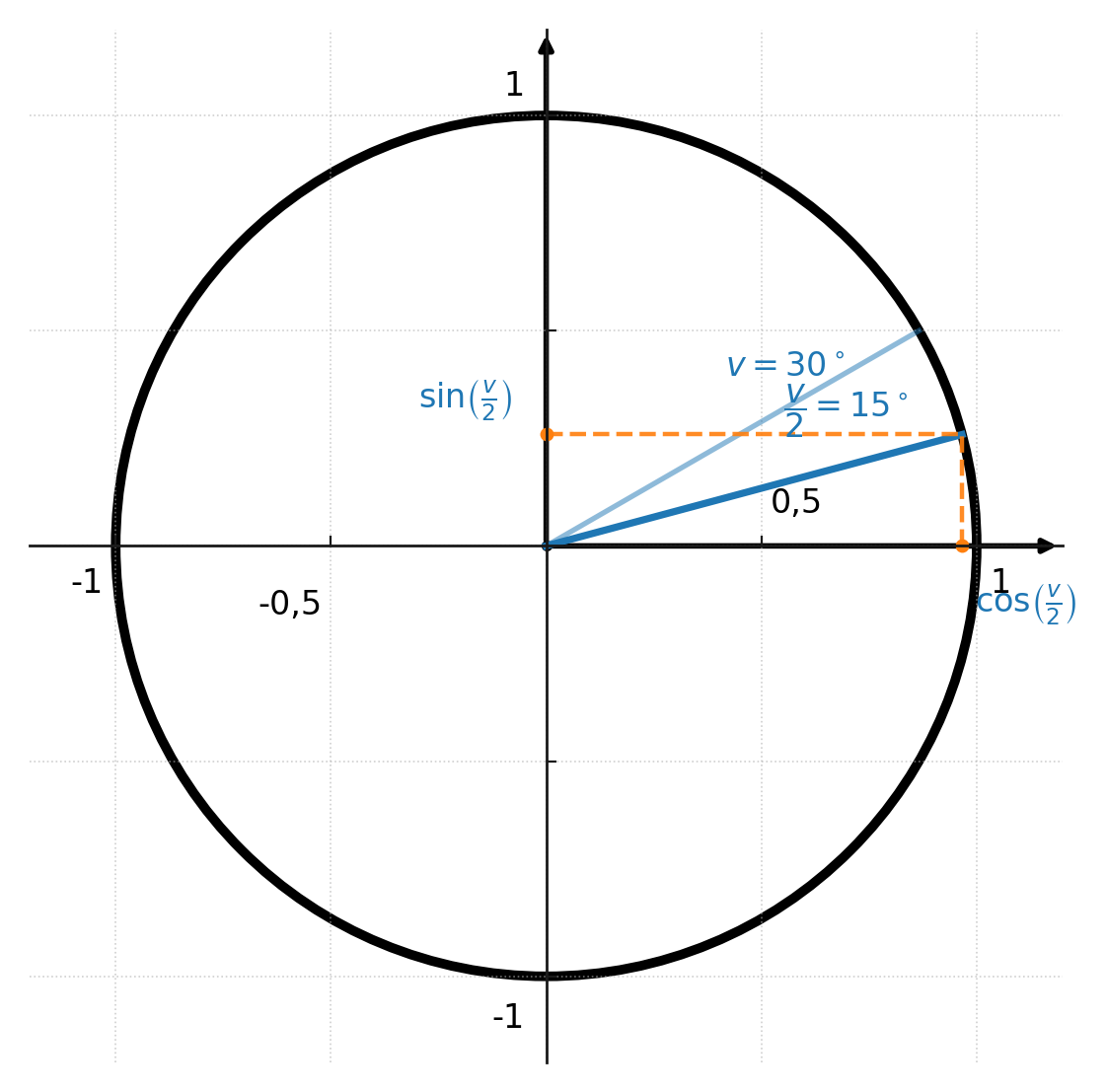
$$ \large \sin\!\left(\tfrac{v}{2}\right) = \pm \sqrt{\tfrac{1 - \cos(v)}{2}} $$

$$ \large \cos\!\left(\tfrac{v}{2}\right) = \pm \sqrt{\tfrac{1 + \cos(v)}{2}} $$

$$ \large \tan\!\left(\tfrac{v}{2}\right) = \tfrac{\sin(v)}{1 + \cos(v)} = \tfrac{1 - \cos(v)}{\sin(v)} $$

Tegnene $+$ eller $-$ afhænger af hvilken kvadrant vinklen befinder sig i.

Trigonometriske relationer halvvinkel

Vi vil beregne $ \sin(2 \cdot 30^\circ) $:

$$ \large \sin(60^\circ) = 2 \cdot \sin(30^\circ) \cdot \cos(30^\circ) $$

$$ \large = 2 \cdot \tfrac{1}{2} \cdot \tfrac{\sqrt{3}}{2} = \tfrac{\sqrt{3}}{2} $$

Formlerne bruges til at finde eksakte værdier for vinkler som 15°, 22.5° og 75°.
De er nyttige i beviser og trigonometriske omskrivninger.
Halvvinkelformlerne bruges ofte til at løse trigonometriske ligninger.