Polygone

Ein Polygon ist eine "Vieleckfigur", also eine Figur mit vielen Seiten.

Was bedeutet also "viele Seiten"?

Es umfasst alle Figuren mit Seiten, einschließlich Dreiecke und Vierecke. Wir haben ihnen eigene Namen gegeben, anstatt einfach zu sagen "ein Polygon mit drei Seiten".

Polygon ist also ein Sammelbegriff für Figuren mit mehreren Seiten.

Verschiedene Polygone

Polygone können entweder konvex oder konkav und regelmäßig oder unregelmäßig sein:

	Konvex	Konkav
Regelmäßig	Alle Winkel sind kleiner als 180^o Alle Seiten sind gleich	Einer oder mehrere Winkel sind größer als 180^o Alle Seiten sind gleich
Unregelmäßig	Alle Winkel sind kleiner als 180^o Seiten sind nicht gleich	Einer oder mehrere Winkel sind größer als 180^o Seiten sind nicht gleich

Figuren

Hier sind die vier Typen als Figuren dargestellt:

	Konvex	Konkav
Regelmäßig
Unregelmäßig

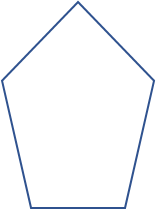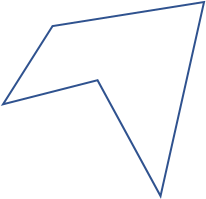Komplexes Polygon

Die vier oben genannten werden alle einfache Polygone genannt, und darüber hinaus gibt es komplexe Polygone, bei denen sich die Linien ebenfalls kreuzen.

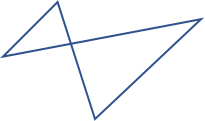
Komplexes Polygon

Winkelsumme im Polygon

Die Winkelsumme in einem Polygon kann mit der folgenden Formel berechnet werden:

$$ Winkelsumme = (Anzahl\ der\ Seiten - 2) \cdot 180 \\[12pt] \Leftrightarrow \\[12pt] \sum \alpha = (n-2)\cdot 180 $$

Wenn du diese Formel bei konkaven Polygonen verwendest, denke daran, dass sie die innere Winkelsumme berechnet.

Fläche

Für regelmäßige konvexe Polygone gibt es eine Formel, mit der man die Fläche berechnen kann:

$$ Fläche=\frac{1}{4} \cdot n \cdot b^2 \cdot cot \biggl( \frac{\pi}{n} \biggr) $$

Wobei $n$ = Anzahl der Seiten und $b$ = Seitenlänge.

Wenn du ein Fünfeck mit einer Seitenlänge von 8 hast, würde es so aussehen:

$$ Fläche=\frac{1}{4} \cdot 5 \cdot 8^2 \cdot cot \biggl( \frac{\pi}{5} \biggr) \Leftrightarrow $$

$$ Fläche=\frac{5 \cdot 64 \cdot 1.376382}{4} \Leftrightarrow $$

$$ Fläche = 110.11 $$

Cot ist Kotangens (Kosinus geteilt durch Sinus). Wenn dein Taschenrechner diese Taste nicht hat, kannst du es so berechnen:

$$ cot \biggl( \frac{\pi}{n} \biggr)= \frac{cos \biggl( \frac{\pi}{n} \biggr)}{sin \biggl( \frac{\pi}{n} \biggr)} $$

Umfang

Für den Umfang gibt es keine besonderen Regeln. Man muss nur die Seitenlängen finden und zusammenzählen.

Im Allgemeinen, wenn man Polygone berechnet und es keine Formel gibt, geht es darum, die Figur in Formen zu unterteilen, die man berechnen kann.

Hier ist es nützlich, einen Überblick über die Trigonometrie zu haben.

Pentagramm

Ein bekanntes komplexes Polygon, das die meisten leicht zeichnen können, ist ein Pentagramm.

Es kann in einem Zug gezeichnet werden, ohne den Stift abzusetzen.

Pentagramm

Das Pentagramm ist ein komplexes Polygon, weil sich die Linien kreuzen.

Das dargestellte Pentagramm ist auch regelmäßig, da alle Seiten gleich lang sind.

Dekagon (Zehnseitiges Polygon)

Das Dekagon unten ist kein komplexes Polygon. Es ist ein regelmäßiges konkaves Polygon.

Dekagon

Es könnte auch unregelmäßig gezeichnet werden. Die innere Winkelsumme des Zehnecks beträgt 1440^o

Namen der Polygone

Anzahl der Seiten	Name	Winkelsumme
3	Trigon	180^o
4	Tetragon	360^o
5	Pentagon	540^o
6	Hexagon	720^o
7	Heptagon	900^o
8	Oktogon	1.080^o
9	Nonagon	1.260^o
10	Dekagon	1.440^o
11	Hendekagon	1.620^o
12	Dodekagon	1.800^o
13	Tridekagon	1.980^o
14	Tetradekagon	2.160^o
15	Pentadekagon	2.340^o
16	Hexadekagon	2.520^o
17	Heptadekagon	2.700^o
18	Oktadekagon	2.880^o
19	Enneadekagon	3.060^o
20	Icosagon	3.240^o
50	Pentacontagon	8.640^o
1.000	Chiliagon	179.640^o
10.000	Myriagon	1.799.640^o