Stetigkeit
Wenn man über das Verhalten von Funktionen spricht, ist eines der wichtigsten Konzepte die Stetigkeit. Stetigkeit beschreibt, ob sich eine Funktion gleichmäßig verändert oder ob Sprünge, Lücken oder abrupte Änderungen im Graphen auftreten. Eine stetige Funktion kann gezeichnet werden, ohne den Stift vom Papier zu heben.
Definition der Stetigkeit
Eine Funktion \( \large f(x) \) ist an einer Stelle \( \large x = a \) stetig, wenn der Grenzwert der Funktion an dieser Stelle gleich dem Funktionswert ist. Dies wird geschrieben als:
$$ \large \lim_{x \to a} f(x) = f(a) $$
Damit eine Funktion an einem Punkt stetig ist, müssen drei Bedingungen erfüllt sein:
- Die Funktion ist an der Stelle \( \large a \) definiert
- Der Grenzwert \( \large \lim_{x \to a} f(x) \) existiert
- Beide Werte sind gleich
Wenn auch nur eine dieser Bedingungen nicht erfüllt ist, ist die Funktion an diesem Punkt nicht stetig.
Arten der Unstetigkeit
Es gibt verschiedene Arten, wie eine Funktion unstetig sein kann. Die wichtigsten Typen sind:
| Typ | Beschreibung |
|---|---|
| Sprungunstetigkeit | Die Funktion springt plötzlich von einem Wert zu einem anderen. |
| Lücke | Der Grenzwert existiert, aber die Funktion ist an diesem Punkt nicht definiert. |
| Unendliche Unstetigkeit | Die Funktion wächst an dieser Stelle unbegrenzt (z. B. bei einer vertikalen Asymptote). |
Diese Arten sind im Graphen deutlich zu erkennen und helfen, das allgemeine Verhalten der Funktion zu verstehen. Das folgende Beispiel zeigt eine Sprungunstetigkeit:
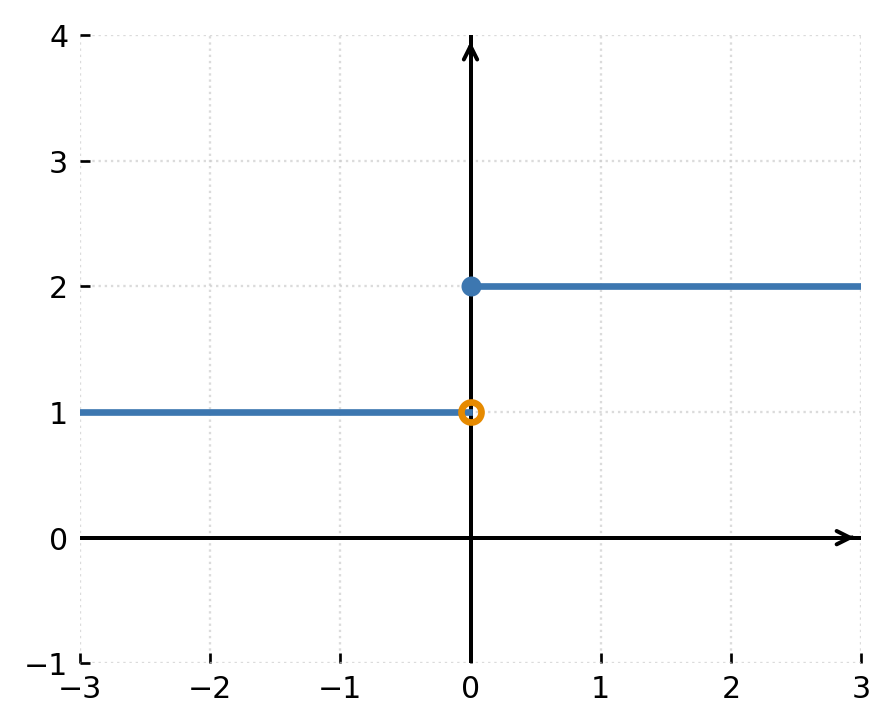
Beispiele
1: Die Funktion \( \large f(x) = 2x + 1 \) ist überall stetig, da man für jedes x einen Wert einsetzen kann, ohne den Graphen zu unterbrechen.
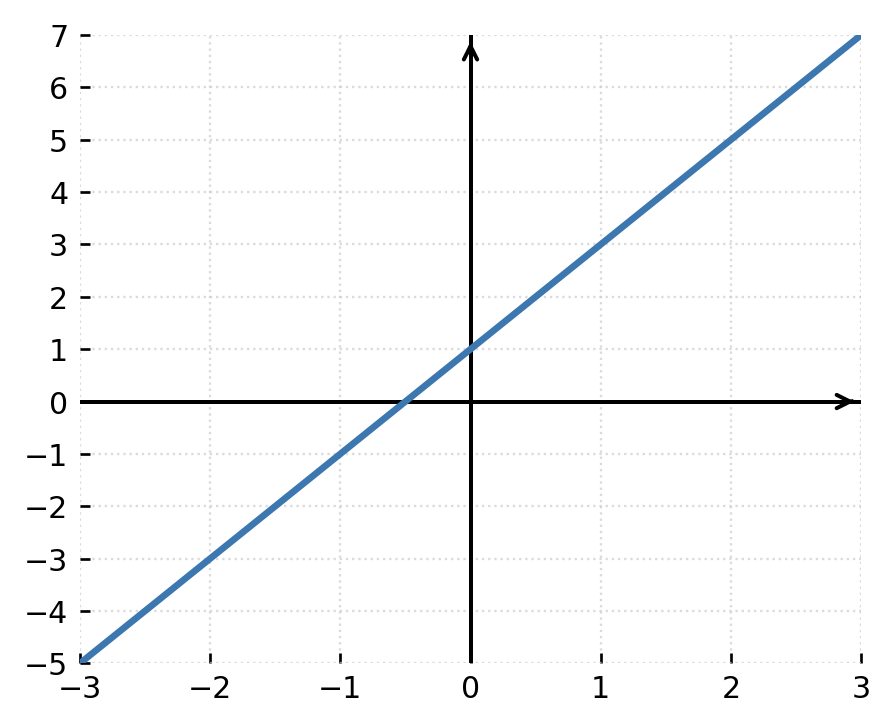
2: Die Funktion
$$ \large f(x) = \frac{x^2 - 9}{x - 3} $$
ist bei \( \large x = 3 \) nicht definiert, aber der Grenzwert an dieser Stelle existiert:
$$ \large \lim_{x \to 3} \frac{x^2 - 9}{x - 3} = 6 $$
Der Graph weist daher eine Lücke im Punkt (3, 6) auf. Die Funktion kann stetig gemacht werden, indem man \( \large f(3) = 6 \) definiert.
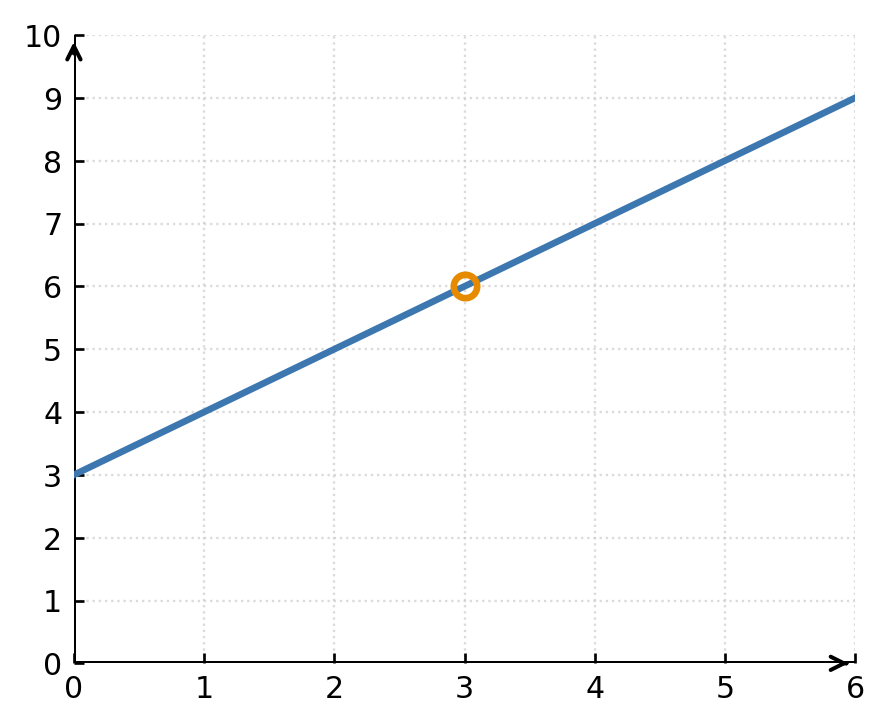
Stetigkeit in einem Intervall
Eine Funktion heißt stetig in einem Intervall, wenn sie an jedem Punkt dieses Intervalls stetig ist. Polynome, Exponential-, Logarithmus- und trigonometrische Funktionen sind Beispiele für Funktionen, die überall dort stetig sind, wo sie definiert sind.
Stetigkeit ist eine wichtige Voraussetzung für viele Sätze der Analysis, darunter den Zwischenwertsatz und Sätze über die Differenzierbarkeit.
Bedeutung in der Analysis
Stetigkeit stellt sicher, dass kleine Änderungen in x kleine Änderungen in f(x) bewirken. Diese Eigenschaft ist entscheidend, um die Ableitung zu definieren, die die Steigung und das lokale Verhalten der Funktion beschreibt. Stetigkeit ist daher ein grundlegender Baustein der gesamten Analysis.