Sekans und Kosekans

Es gibt auch zwei reziproke Funktionen, nämlich die Sekans und die Kosekans. Sie werden als die Kehrwerte von Kosinus und Sinus definiert:

 

$$ \large \sec(v) = \tfrac{1}{\cos(v)} \qquad \csc(v) = \tfrac{1}{\sin(v)} $$

 

Das bedeutet: Wenn man den Kosinus oder Sinus eines Winkels kennt, kann man die Sekans oder die Kosekans bestimmen, indem man einfach den Kehrwert nimmt.

Zum Beispiel, wenn der Winkel 25° beträgt:

 

$$ \large \cos(25^\circ) \approx 0.906 \quad \Rightarrow \quad \sec(25^\circ) \approx 1.103 $$

$$ \large \sin(25^\circ) \approx 0.423 \quad \Rightarrow \quad \csc(25^\circ) \approx 2.366 $$

 

Im Einheitskreis können Sekans und Kosekans ebenfalls grafisch dargestellt werden.

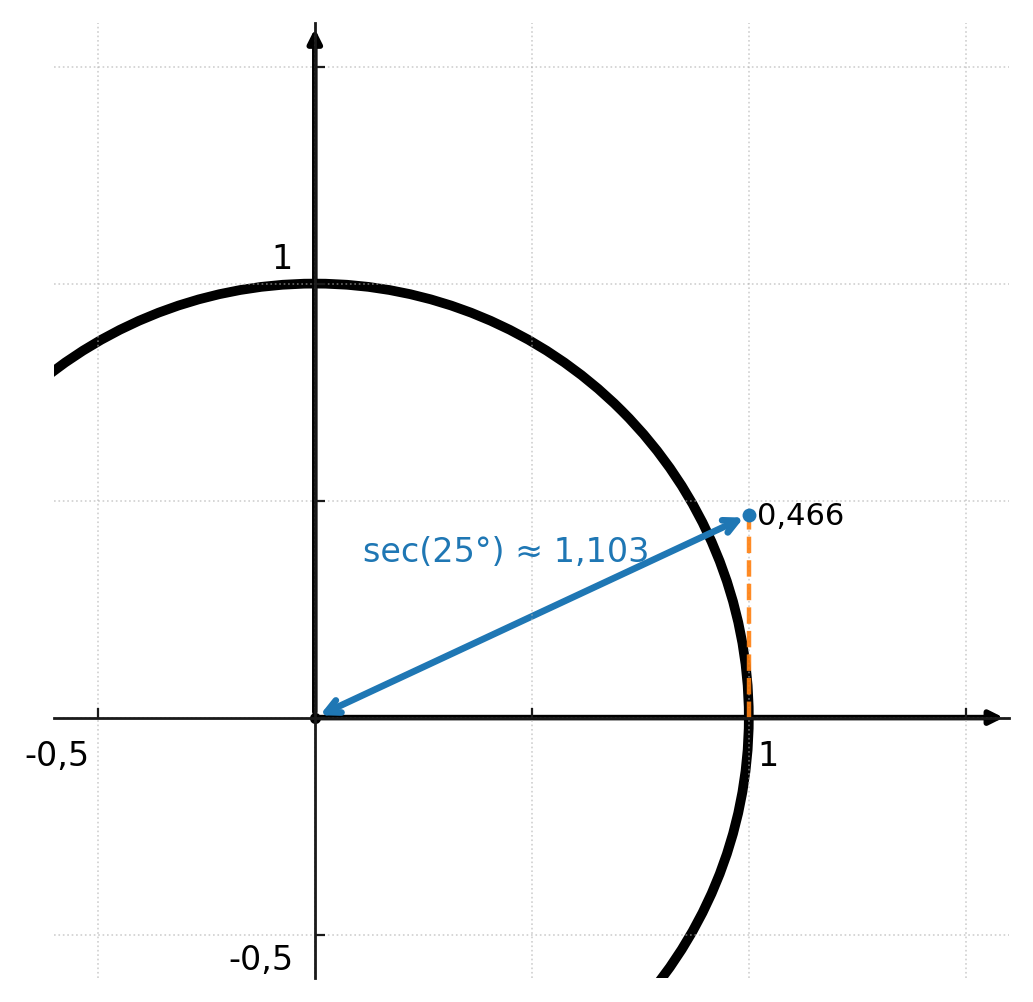
Beide Funktionen erhält man, indem man den Strahl des Winkels verlängert, bis er die Linie x = 1 (für die Sekans) oder die Linie y = 1 (für die Kosekans) schneidet.

Der Abstand vom Zentrum bis zum Schnittpunkt ist der Wert der Funktion. Die Abbildung unten zeigt, dass der Tangens 0,466 und die Sekans 1,103 beträgt.

 

 

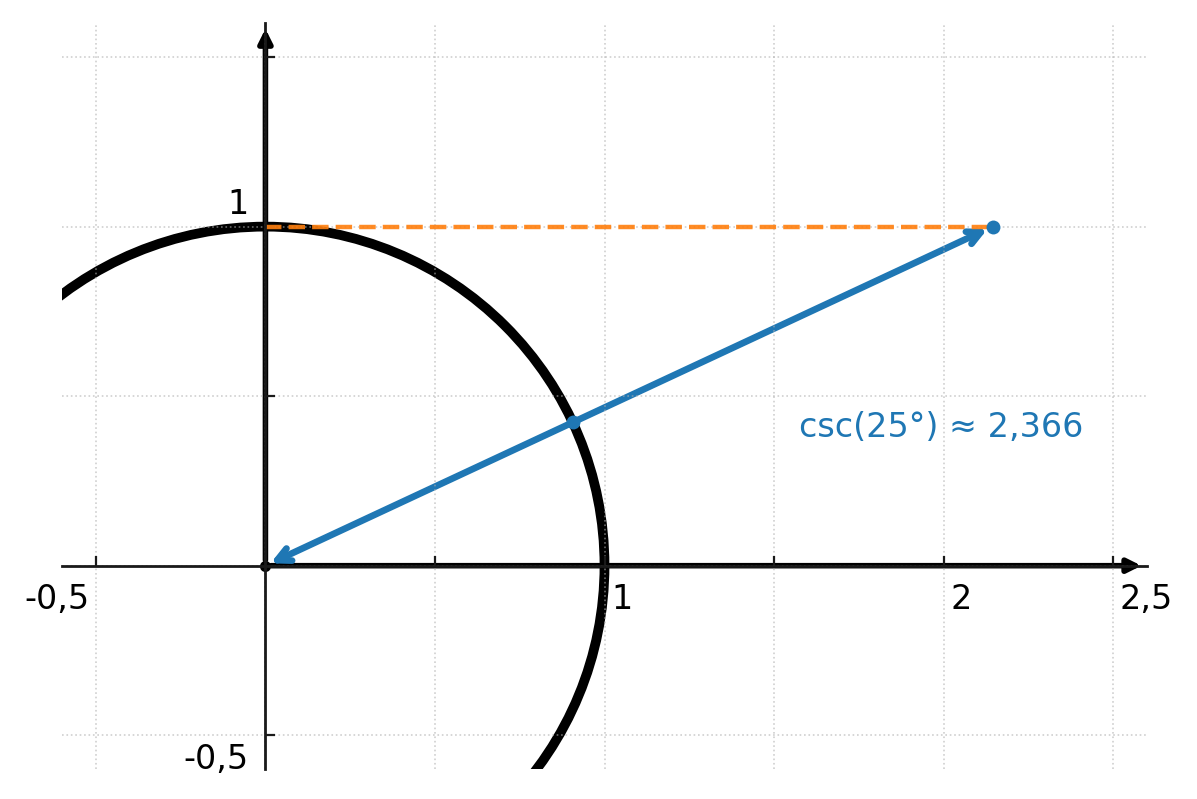
Hier ist die Kosekans im Einheitskreis für den Winkel von 25 Grad dargestellt, wobei die Länge vom Zentrum bis zum Schnittpunkt 2,366 beträgt

 

 

Anwendung

Sekans und Kosekans sind besonders nützlich, zum Beispiel in der Differentialrechnung und in anderen fortgeschrittenen Bereichen der Mathematik, wo sie bestimmte Berechnungen vereinfachen.

In der elementaren Geometrie beschränkt man sich normalerweise auf Sinus, Kosinus und Tangens.

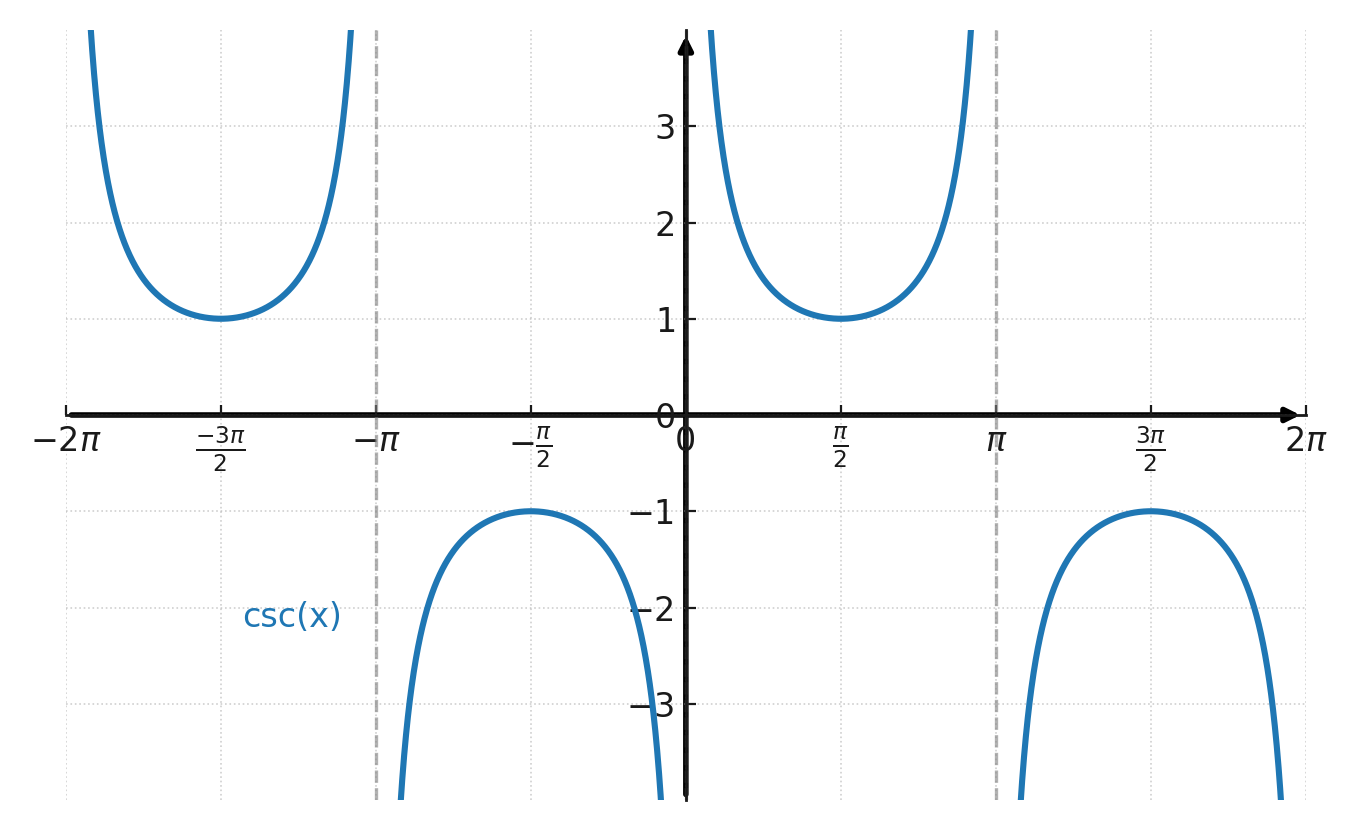
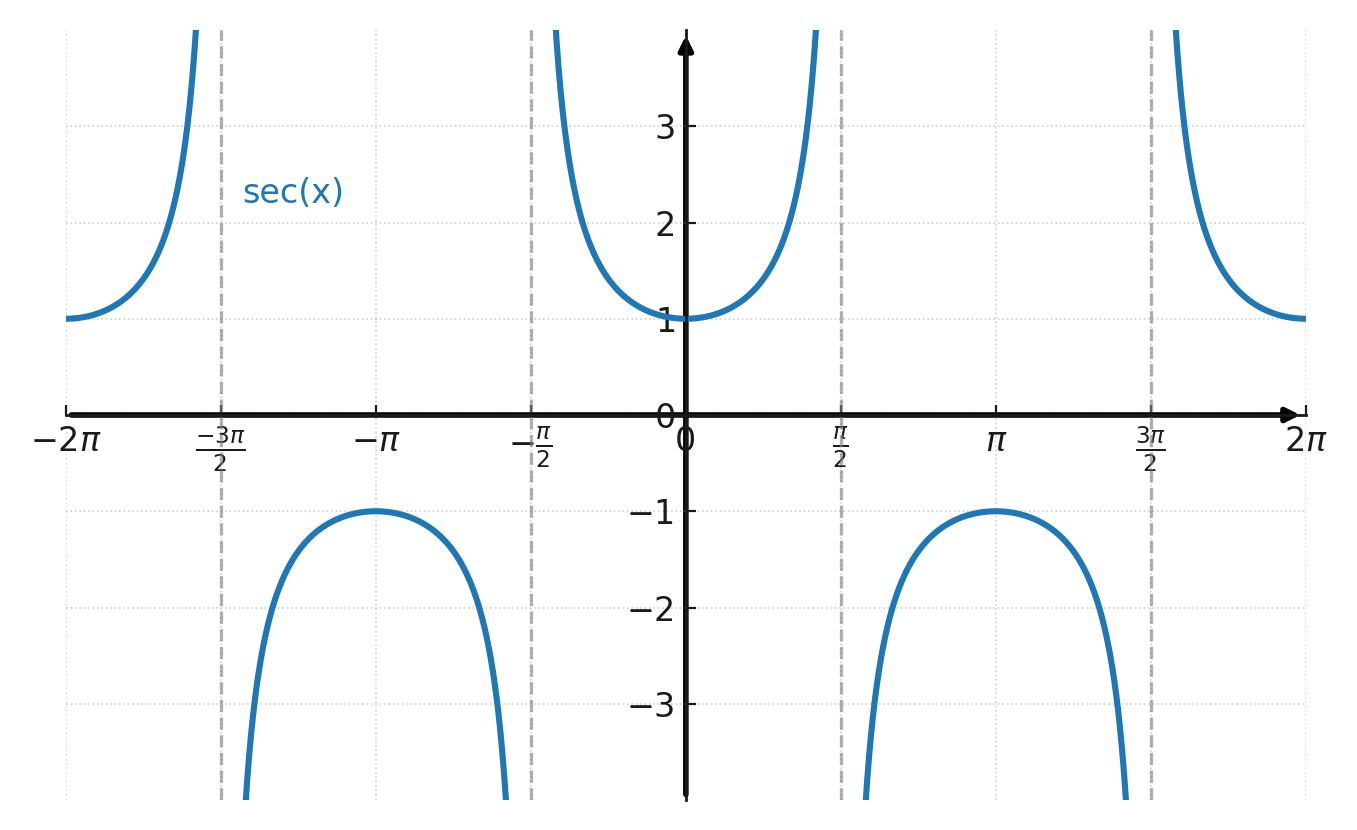
Ein schneller Blick auf die Graphen von Sekans und Kosekans erklärt warum. Die Funktionen haben vertikale Asymptoten, springen zu sehr großen Werten und sind nicht überall definiert, im Gegensatz zu Sinus und Kosinus.

 

Graph der Sekans:

 

Graph der Kosekans: