Poisson-fordelingen er en sandsynlighedsfordeling, der beskriver sandsynligheden for et bestemt antal hændelser i et givet tidsrum eller område, når hændelserne sker uafhængigt af hinanden og med en konstant gennemsnitlig frekvens. Den bruges ofte til at modellere sjældne hændelser.

Definition

En stokastisk variabel \(\large X\) siges at være Poisson-fordelt med parameter \(\large \lambda\), hvis den har sandsynlighedsfunktionen:

$$ \large P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!}, \quad k = 0, 1, 2, \dots $$

Her er \(\large \lambda\) det gennemsnitlige antal hændelser i tidsrummet eller området.

Egenskaber

• Middelværdi: \( E(X) = \lambda \)
• Varians: \( Var(X) = \lambda \)
• Kun én parameter \(\lambda\), der bestemmer både gennemsnit og spredning
• Diskret fordeling (defineret for \(k = 0,1,2, \dots\))

Eksempel

Antag at antallet af mails, en person modtager på en time, er Poisson-fordelt med \(\large \lambda = 5\).

Hvad er sandsynligheden for at modtage præcis 3 mails på en time?

$$ \large P(X = 3) = \frac{5^3 \cdot e^{-5}}{3!} $$

$$ \large P(X = 3) = \frac{125 \cdot e^{-5}}{6} $$

$$ \large P(X = 3) \approx 0,1404 $$

Der er altså ca. 14% sandsynlighed for at modtage præcis 3 mails på en time.

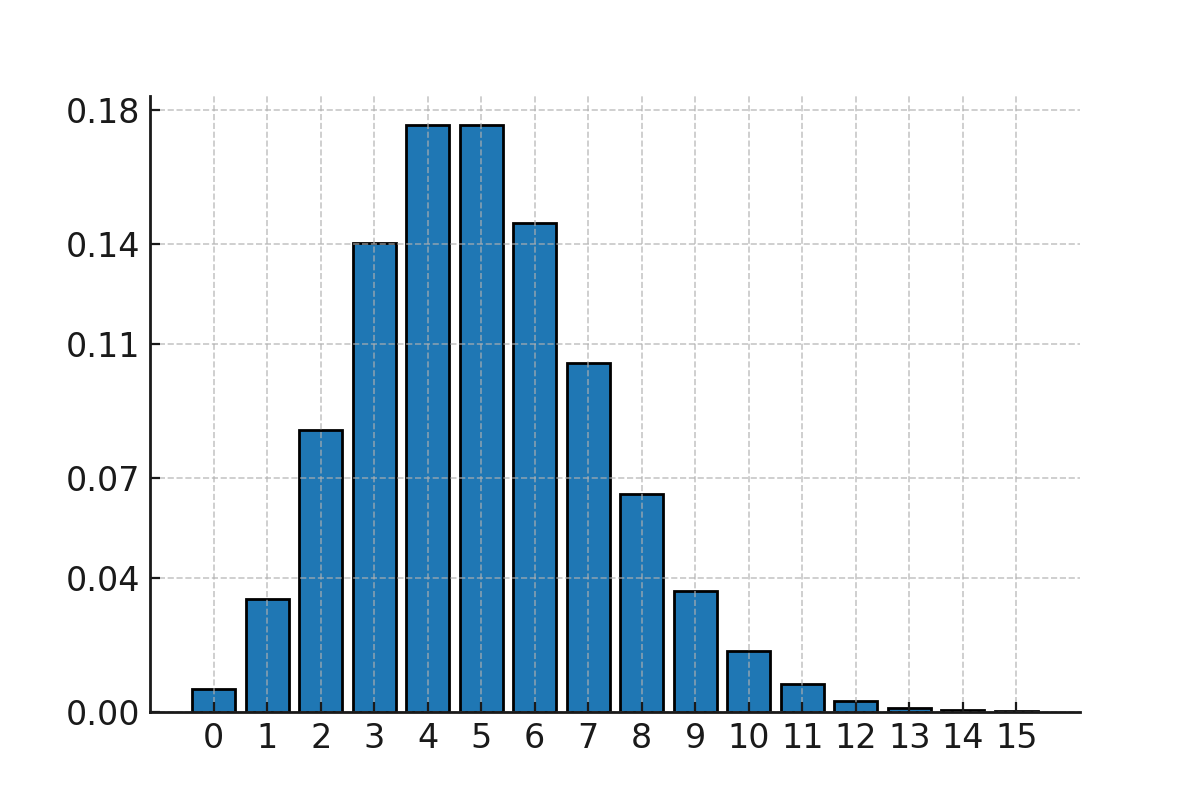
Graf

Poisson-fordelingen kan vises som et søjlediagram, hvor sandsynligheden for hvert muligt udfald \(\large k\) tegnes. Fordelingen er typisk skæv, men bliver mere symmetrisk, når \(\large \lambda\) vokser.

Forhold til binomialfordelingen

Poisson-fordelingen kan ses som en tilnærmelse til binomialfordelingen. Hvis antallet af forsøg \(\large n\) er meget stort, og sandsynligheden for succes \(\large p\) er meget lille, kan binomialfordelingen \( B(n,p) \) tilnærmes af en Poisson-fordeling med parameter:

$$ \large \lambda = n \cdot p $$

Denne sammenhæng gør Poisson-fordelingen særligt nyttig i situationer med sjældne hændelser, hvor binomialfordelingen ville være tung at beregne.