Binomialfordelingen
Binomialfordelingen er en sandsynlighedsfordeling, der beskriver, hvor sandsynligt det er at få et bestemt antal successer i en række uafhængige forsøg.
Et forsøg har kun to mulige udfald: succes eller fiasko. Eksempler kan være plat eller krone, ramme eller misse, bestå eller dumpe.
Forudsætninger
- Der udføres et fast antal forsøg, \( \large n \).
- Hvert forsøg har to udfald: succes eller fiasko.
- Sandsynligheden for succes er den samme i hvert forsøg, \( \large p \).
- Forsøgene er uafhængige af hinanden.
Formlen
Sandsynligheden for at få præcist \( \large r \) successer i \( \large n \) forsøg er:
$$ \large P(X=r) = \binom{n}{r} p^r (1-p)^{n-r} $$
Her er \(\large \binom{n}{r}\) en kombination, som angiver hvor mange måder man kan placere de \( \large r \) successer blandt de \( \large n \) forsøg.
Eksempel 1: Møntkast
En mønt kastes 10 gange. Sandsynligheden for at få plat er \( \large p = 0.5 \).
Hvad er sandsynligheden for at få præcist 6 gange plat?
$$ \large P(X=6) = \binom{10}{6} (0.5)^6 (0.5)^{4} $$
$$ \large P(X=6) = 210 \cdot (0.5)^{10} $$
$$ \large P(X=6) \approx 0.205 $$
Der er altså ca. 20,5% sandsynlighed for at få 6 gange plat.
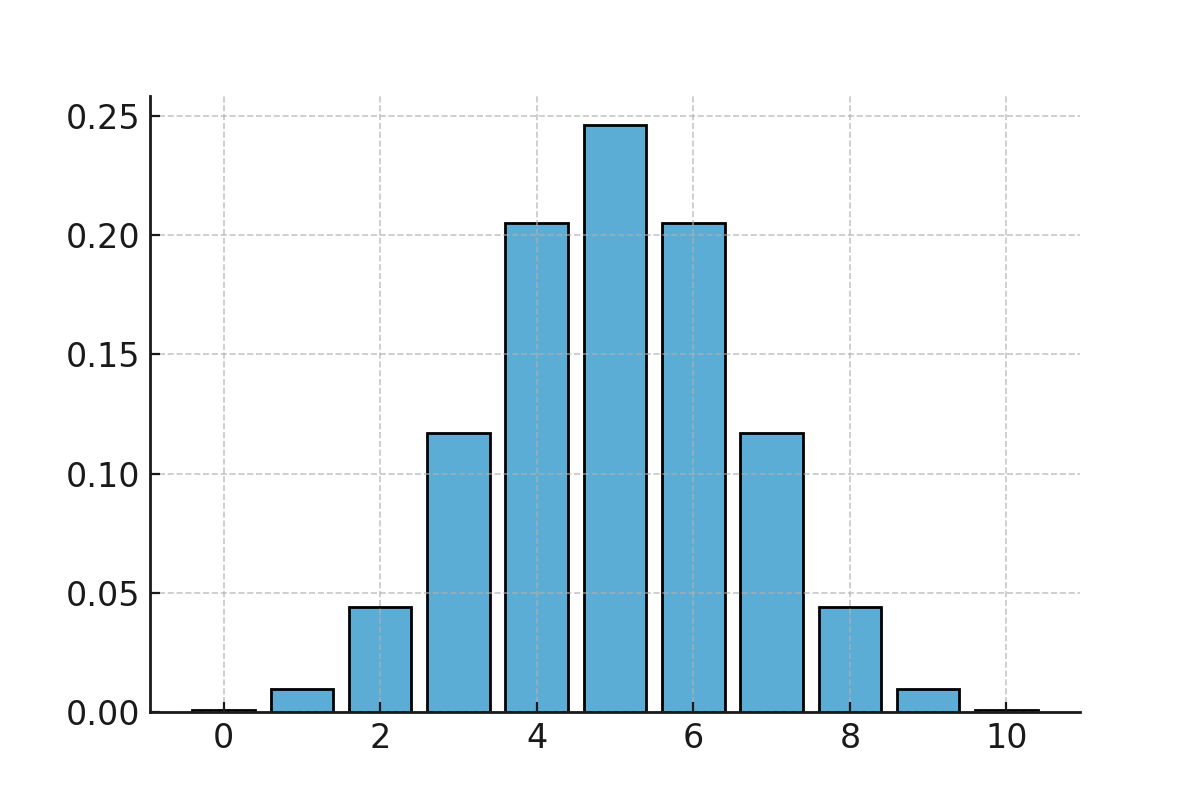
Binomialfordelingen ved kast med en mønt
Eksempel 2: Terning
En terning kastes 5 gange. Vi definerer succes som at få en sekser. Her er \( \large p = \tfrac{1}{6} \).
Sandsynligheden for at få præcist 2 seksere er:
$$ \large P(X=2) = \binom{5}{2} \left(\tfrac{1}{6}\right)^2 \left(\tfrac{5}{6}\right)^3 $$
$$ \large P(X=2) = 10 \cdot \tfrac{1}{36} \cdot \tfrac{125}{216} $$
$$ \large P(X=2) = \tfrac{1250}{7776} $$
$$ \large P(X=2) \approx 0.161 $$
For at få overblik kan vi beregne sandsynlighederne for alle de mulige udfald:
| \( \large r \) | Sandsynlighed \( \large P(X=r) \) |
|---|---|
| 0 | \( \large 0.401 \) |
| 1 | \( \large 0.402 \) |
| 2 | \( \large 0.161 \) |
| 3 | \( \large 0.032 \) |
| 4 | \( \large 0.003 \) |
| 5 | \( \large 0.00013 \) |
Vi ser at det er mest sandsynligt at få 0 eller 1 sekser i 5 kast, og at sandsynligheden hurtigt bliver meget lille for højere antal.
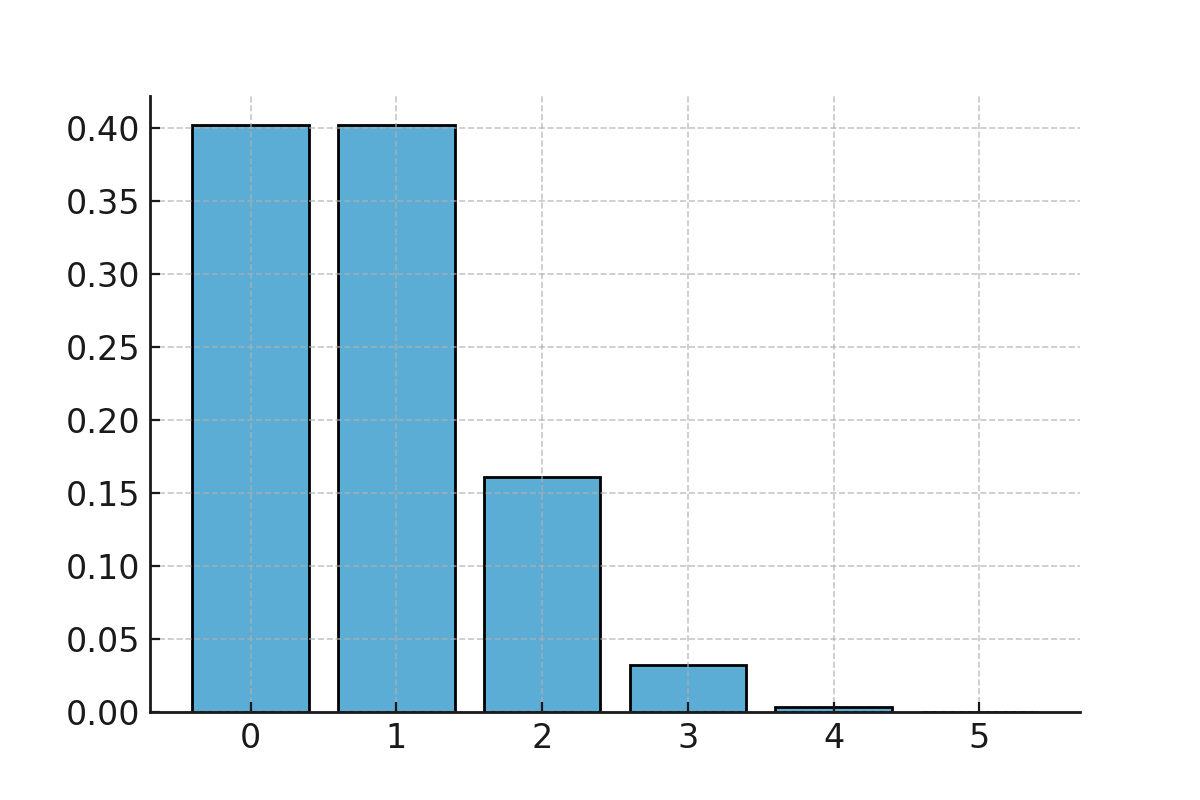
Binomialfordelingen ved kast med en terning
Eksempel 3: Kvalitetskontrol
I en fabrik er 5% af produkterne defekte. Vi udtager 20 produkter tilfældigt. Sandsynligheden for at finde præcist 3 defekte er:
$$ \large P(X=3) = \binom{20}{3} (0.05)^3 (0.95)^{17} $$
$$ \large P(X=3) = 1140 \cdot (0.000125) \cdot (0.419) $$
$$ \large P(X=3) \approx 0.059 $$
For at få overblik kan vi beregne sandsynlighederne for 0 til 5 defekte produkter:
| \( \large r \) | Sandsynlighed \( \large P(X=r) \) |
|---|---|
| 0 | \( \large 0.358 \) |
| 1 | \( \large 0.377 \) |
| 2 | \( \large 0.188 \) |
| 3 | \( \large 0.059 \) |
| 4 | \( \large 0.014 \) |
| 5 | \( \large 0.003 \) |
Vi ser at det mest sandsynlige er at finde 0 eller 1 defekt, men der er stadig en reel sandsynlighed for at finde 2 eller 3 defekte i en stikprøve.
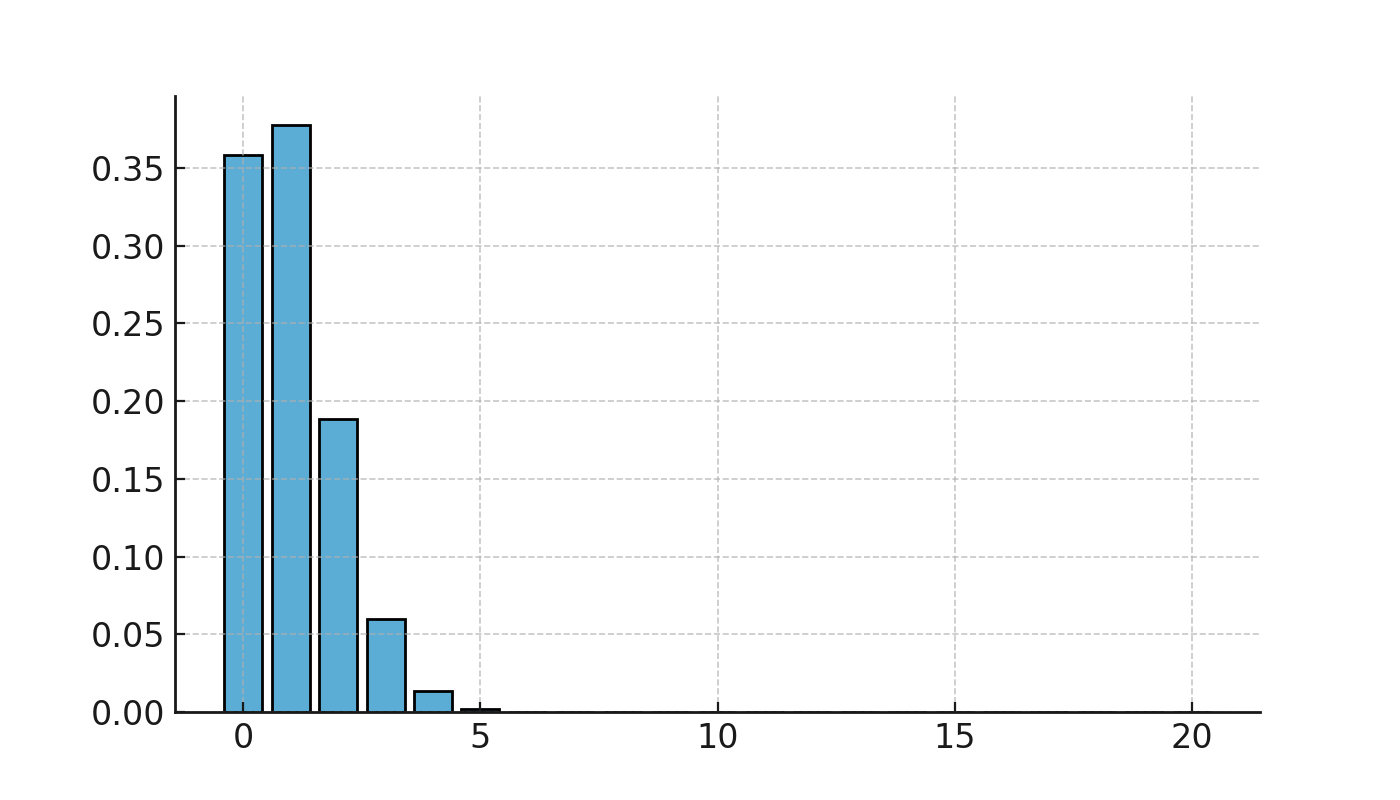
Binomialfordelingen ved kvalitetskontrol
Egenskaber
- Middelværdi: \( \large \mu = n \cdot p \)
- Varians: \( \large \sigma^2 = n \cdot p \cdot (1-p) \)
- Standardafvigelse: \( \large \sigma = \sqrt{n \cdot p \cdot (1-p)} \)
Binomial og normalfordeling
Når \( \large n \) er stort, og \( \large p \) ikke er alt for tæt på 0 eller 1, kan binomialfordelingen tilnærmes med en normalfordeling:
$$ \large N(\mu, \sigma^2) = N(n \cdot p, n \cdot p \cdot (1-p)) $$
Dette er nyttigt, fordi normalfordelingen er lettere at regne med ved store \( \large n \).
Anvendelser
- Statistik: modellering af forsøg med to udfald.
- Biologi: sandsynligheden for at et bestemt antal planter spirer.
- Medicin: sandsynligheden for at et bestemt antal patienter reagerer på en behandling.
- Kvalitetskontrol: hvor mange defekte produkter findes i en stikprøve.
- Spil og simulationer: fx møntkast, terningekast eller andre eksperimenter med gentagne forsøg.
Opsummering
- Binomialfordelingen beskriver sandsynligheden for et bestemt antal successer i \( \large n \) uafhængige forsøg.
- Ved store \( \large n \) kan binomialfordelingen tilnærmes af en normalfordeling.
- Den har mange anvendelser i statistik, sandsynlighedsregning, biologi, medicin, spil og kvalitetskontrol.
Binomialfordelingen er en af de mest fundamentale fordelinger i sandsynlighedsteorien og forbinder kombinatorik med statistik.