Normalfordelingen er en af de vigtigste sandsynlighedsfordelinger i statistik. Den bruges til at beskrive mange fænomener i naturen og samfundet, hvor data fordeler sig omkring et gennemsnit. Eksempler er højder, målefejl og karaktergennemsnit.

 

Definition

En stokastisk variabel \(\large X\) siges at være normalfordelt med middelværdi \(\large \mu\) og varians \(\large \sigma^2\), hvis den har tæthedsfunktionen:

 

$$ \large f(x) = \frac{1}{\sigma \sqrt{2\pi}} \, e^{-\frac{(x-\mu)^2}{2\sigma^2}}, \quad -\infty < x < \infty $$

 

Her er \(\large \mu\) fordelingens centrum (middelværdien), og \(\large \sigma\) bestemmer hvor spredt værdierne ligger omkring dette centrum.

 

Egenskaber

 

• Middelværdi: \( \mu \)
• Varians: \( \sigma^2 \)
• Standardafvigelse: \( \sigma \)
• Symmetrisk omkring middelværdien
• Klokkeformet kurve, der aldrig rører x-aksen

 

 

Standardnormalfordelingen

Hvis man sætter \( \large \mu = 0 \) og \( \large \sigma = 1 \), får man standardnormalfordelingen:

 

$$ \large Z \sim N(0,1) $$

 

En vilkårlig normalfordelt variabel kan omskrives til en standardnormal via transformationen:

 

$$ \large Z = \frac{X - \mu}{\sigma} $$

 

Standardnormalfordelingen bruges, fordi der findes tabeller og computerfunktioner til at beregne sandsynligheder ud fra \(\large Z\).

 

 

Eksempel

Antag at højden for voksne mænd er normalfordelt med middelværdi \(\large \mu = 180\) cm og standardafvigelse \(\large \sigma = 10\) cm.

 

Hvad er sandsynligheden for at en tilfældig mand er mellem 170 og 190 cm høj?

 

Vi omskriver til standardnormalen:

 

$$ \large Z_1 = \frac{170 - 180}{10} = -1 $$

$$ \large Z_2 = \frac{190 - 180}{10} = 1 $$

 

Sandsynligheden er dermed:

 

$$ \large P(170 \leq X \leq 190) = P(-1 \leq Z \leq 1) = F(1) - F(-1) $$

 

hvor \(F(z)\) er den kumulerede fordelingsfunktion:

 

$$ \large F(z) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{z} e^{-\tfrac{t^2}{2}} \, dt $$

 

Integralets værdi kan ikke beregnes i lukket form, men det kan aflæses i tabeller. For \(\large z = 1\) og \(\large z = -1\) har man:

 

$$ \large F(1) \approx 0,8413 \quad \text{og} \quad F(-1) \approx 0,1587 $$

 

Dermed bliver sandsynligheden:

 

$$ \large P(-1 \leq Z \leq 1) = 0,8413 - 0,1587 = 0,6826 $$

 

Altså ligger ca. 68% af alle observationer inden for én standardafvigelse af middelværdien.

 

 

68-95-99,7-reglen

En vigtig tommelfingerregel for normalfordelingen er, at sandsynlighederne fordeler sig på en bestemt måde omkring middelværdien:

 

• Ca. 68% af alle observationer ligger inden for 1 standardafvigelse (\(\large \mu \pm 1\sigma\))
• Ca. 95% ligger inden for 2 standardafvigelser (\(\large \mu \pm 2\sigma\))
• Ca. 99,7% ligger inden for 3 standardafvigelser (\(\large \mu \pm 3\sigma\))

 

Reglen viser, at de fleste observationer ligger tæt på middelværdien, mens ekstreme værdier er meget sjældne.

 

 

Graf

Kurven for normalfordelingen har den velkendte klokkeform og viser fordelingen med middelværdien i centrum og aftagende sandsynlighed til begge sider.

 

 

 

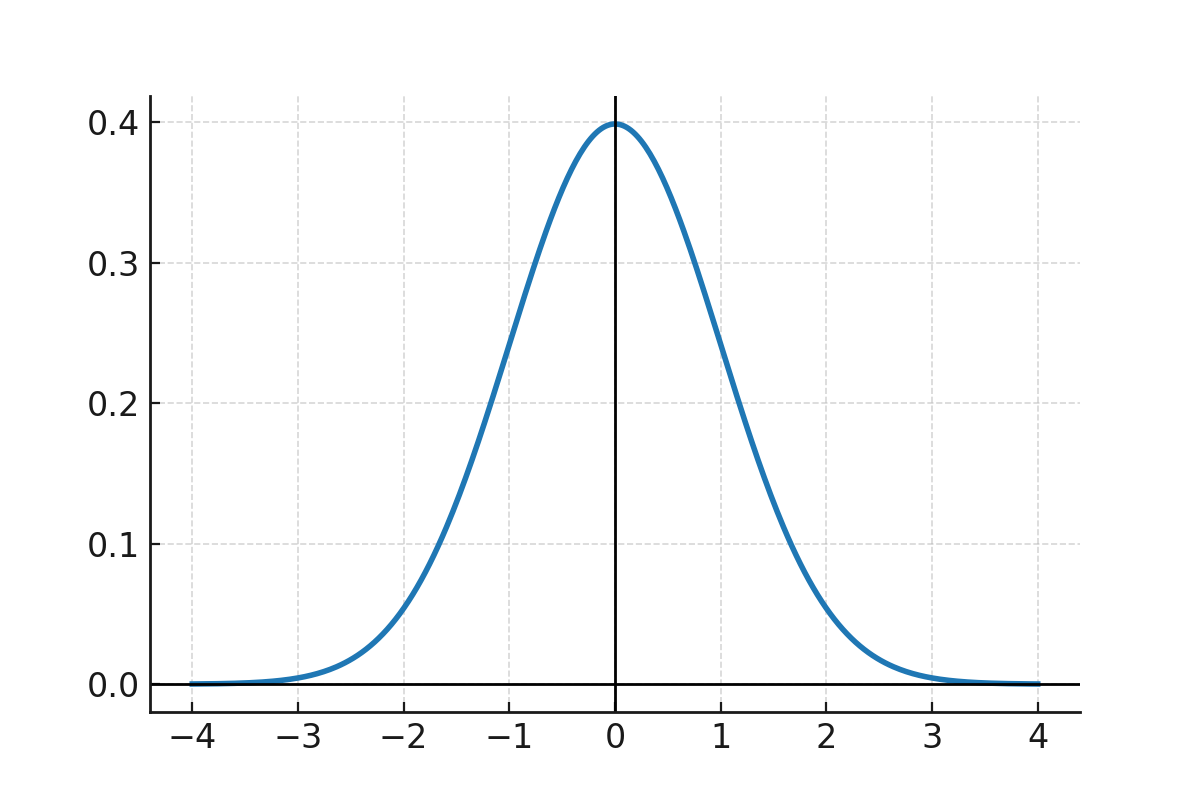
Kurven viser tæthedsfunktionen. Højden på kurven er ikke en sandsynlighed i sig selv, men sandsynligheder findes ved at beregne arealet under kurven i et interval.

For standardnormalfordelingen topper tæthedsfunktionen i middelværdien med værdien:

 

$$ \large f(0) = \frac{1}{\sqrt{2\pi}} \approx 0,3989 $$

 

Dette betyder at grafen når op til ca. 0,4 på y-aksen. Det stemmer overens med definitionen, og er ikke en sandsynlighed i sig selv.

Eksempelvis giver sandsynligheden for at ligge inden for ét standardafvigelse af middelværdien et areal under kurven på ca. 68%, selv om højden af kurven ved \(\large \mu\) er ca. 0,4.

 

 

Forhold til binomialfordelingen

Når antallet af forsøg \(\large n\) i en binomialfordeling er stort, og sandsynligheden \(\large p\) ikke er for tæt på 0 eller 1, kan binomialfordelingen tilnærmes med en normalfordeling:

 

$$ \large X \sim N(n \cdot p,\; n \cdot p \cdot (1-p)) $$

 

Her bruger man ofte en såkaldt kontinuitetskorrektion, hvor man justerer grænserne med 0,5 for at tage højde for at binomialfordelingen er diskret og normalfordelingen kontinuert.