Types et rôles de vecteurs

Les vecteurs peuvent avoir différents rôles selon le contexte. Certains sont utilisés pour décrire des directions, d’autres pour indiquer une direction perpendiculaire ou pour constituer la base d’un système de coordonnées entier. Ici, nous examinons les types de vecteurs les plus importants.

 

 

Vecteurs directeurs

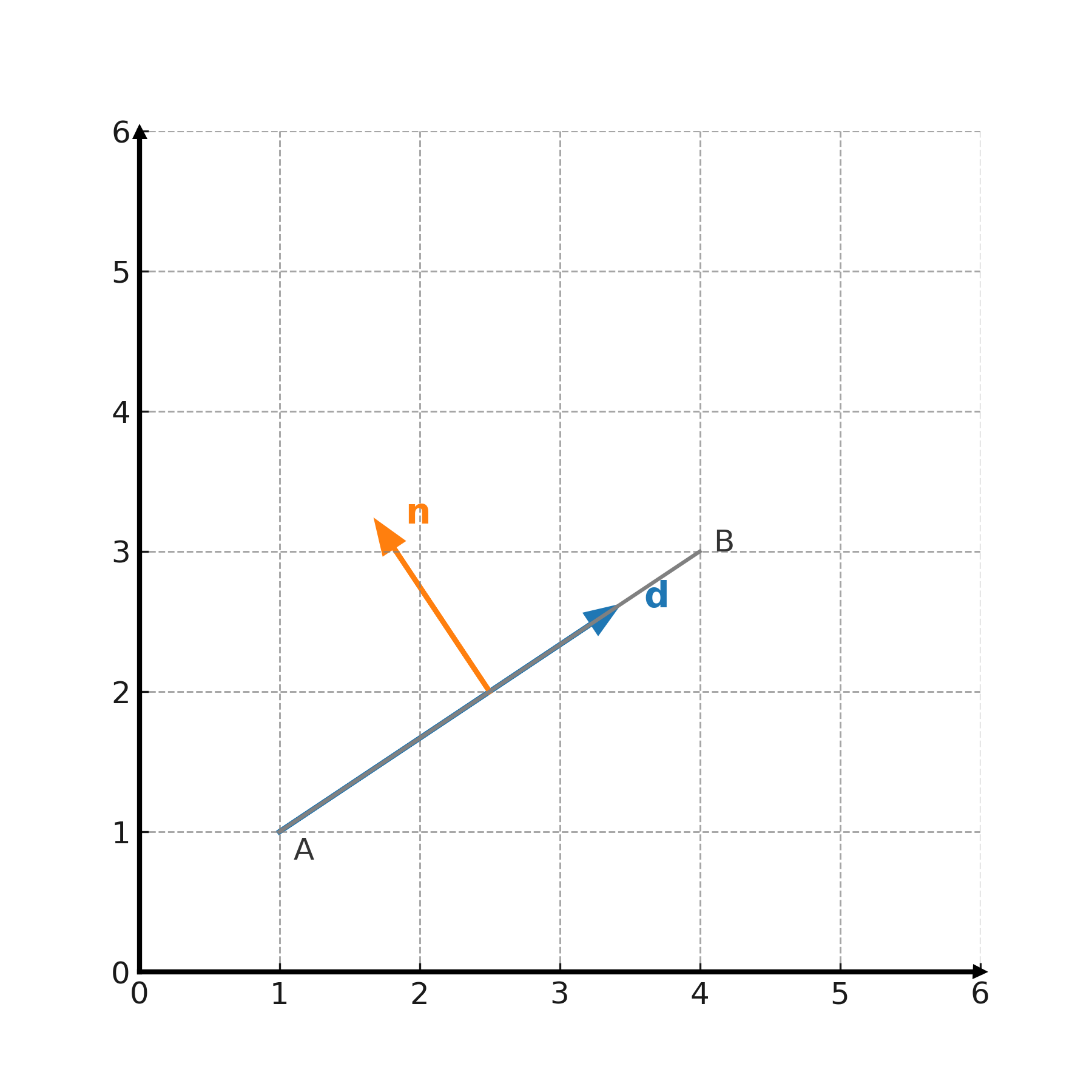
Un vecteur directeur (d) décrit la direction d’une droite ou d’un plan. Si une droite passe par les points \( \large A=(x_1,y_1) \) et \( \large B=(x_2,y_2) \), alors

 

$$ \large \mathbf{d} = (x_2-x_1,\; y_2-y_1) $$

 

est un vecteur directeur de la droite. Avec un vecteur directeur, on peut écrire une représentation paramétrique :

 

$$ \large (x,y) = (x_1,y_1) + t \cdot \mathbf{d}, \quad t \in \mathbb{R} $$

 

ce qui décrit tous les points de la droite.

 

 

Vecteurs normaux

Un vecteur normal est perpendiculaire à une droite ou à un plan. Si la droite a pour vecteur directeur \( \large (a,b) \), alors

 

$$ \large \mathbf{n} = (-b,a) \quad \text{ou} \quad (b,-a) $$

 

sont des vecteurs normaux. Un vecteur normal peut être utilisé pour écrire une droite sous la forme

 

$$ \large n_1 \cdot x + n_2 \cdot y + c = 0 $$

 

où \( \large (n_1,n_2) \) est le vecteur normal. Qu’un vecteur soit normal peut se tester à l’aide du produit scalaire : Si \( \large \mathbf{r} \cdot \mathbf{n} = 0 \), alors ils sont perpendiculaires.

 

 

Vecteurs unitaires

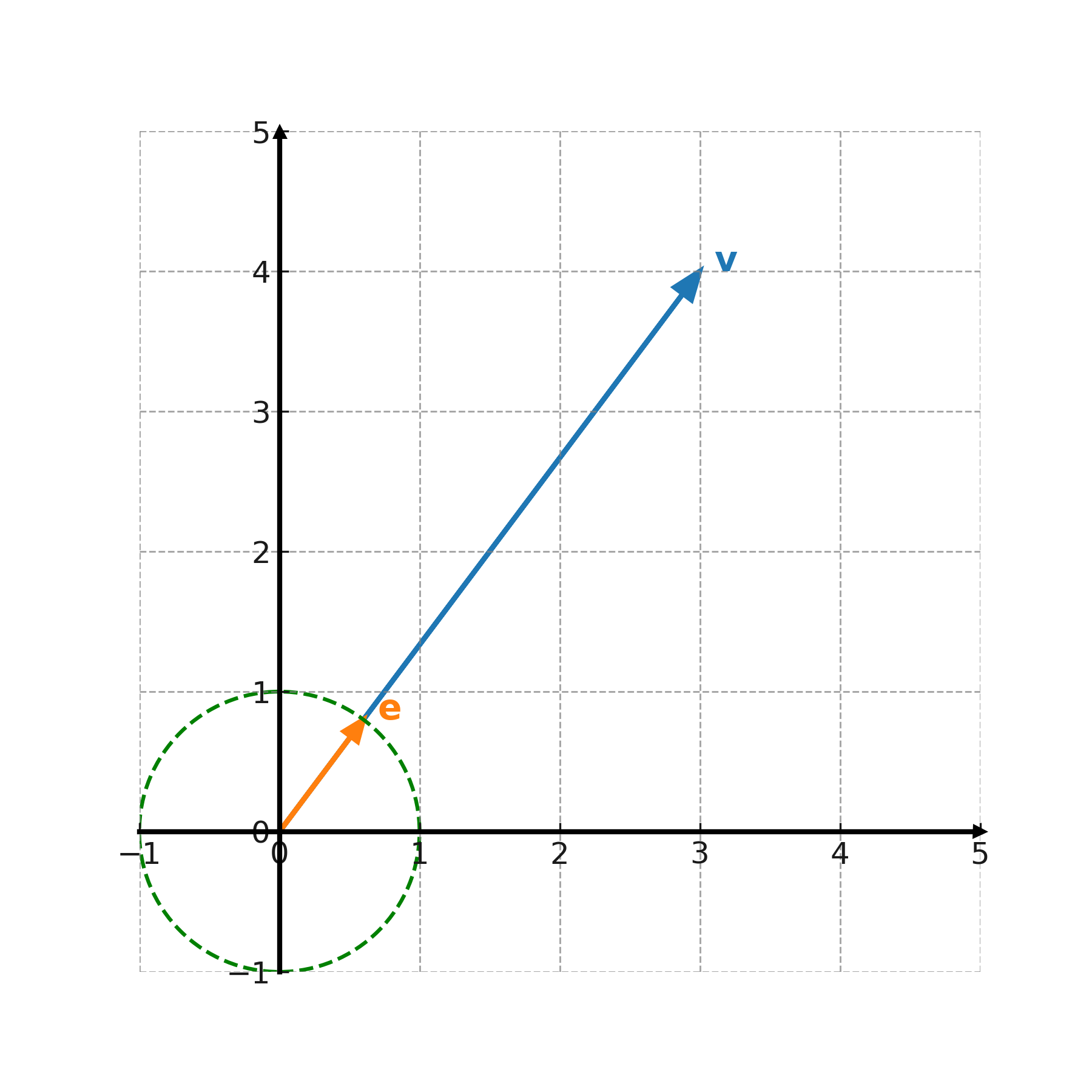
Un vecteur unitaire a une longueur de 1 et est utilisé pour décrire une direction pure. Tout vecteur peut devenir un vecteur unitaire en le divisant par sa longueur :

 

$$ \large \mathbf{e} = \frac{1}{|\mathbf{v}|} \cdot \mathbf{v} $$

 

Les vecteurs unitaires sont utilisés, par exemple, pour définir la direction des axes dans un système de coordonnées.

 

 

Vecteurs tangents

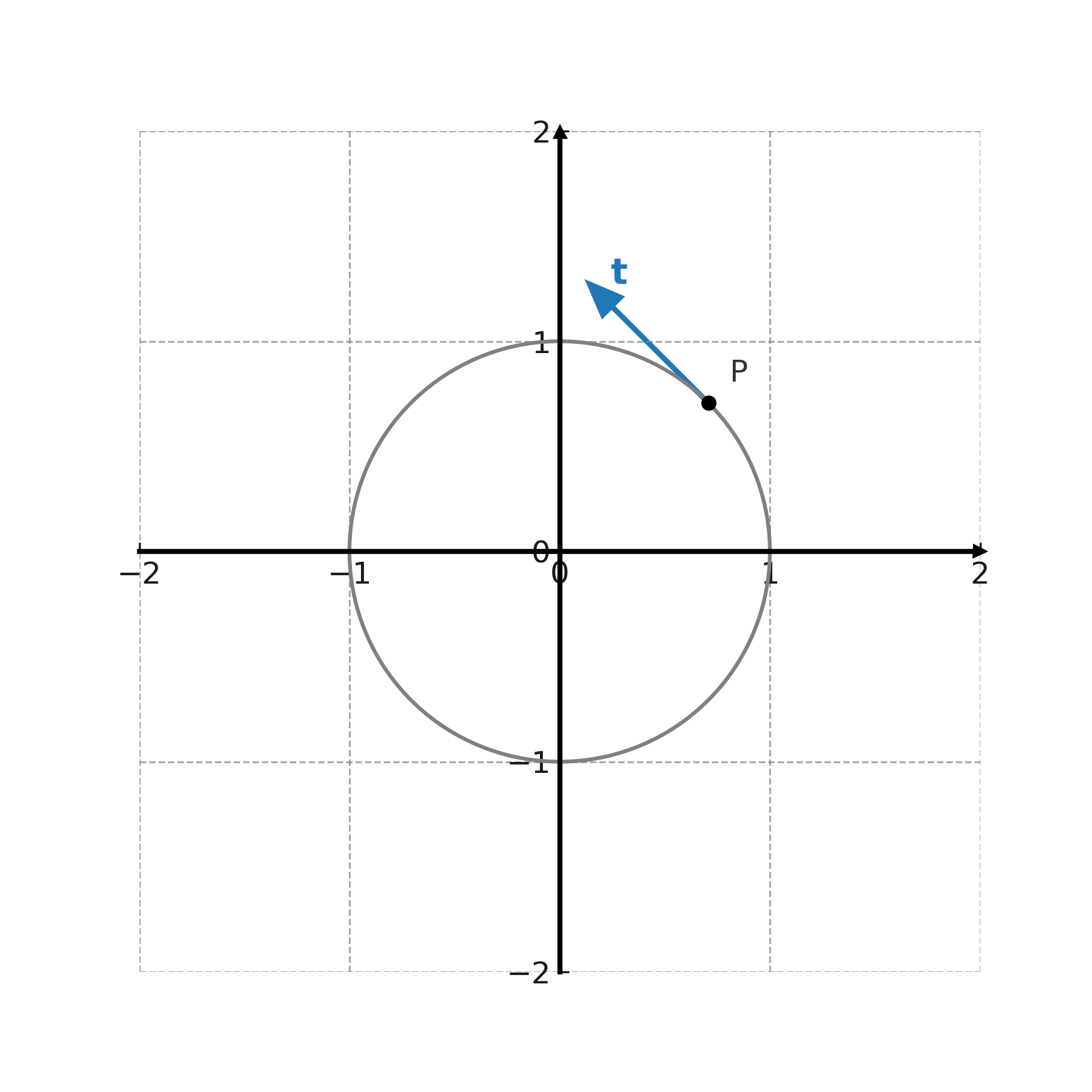
Dans le cadre des courbes, les vecteurs tangents sont utilisés pour décrire la direction en un point donné. Pour une courbe différentiable \( \large (x(t),y(t)) \), le vecteur tangent est donné par

 

$$ \large \mathbf{t} = \big(x'(t),\,y'(t)\big) $$

 

ce qui montre comment la courbe évolue au point.

 

Vecteurs de base

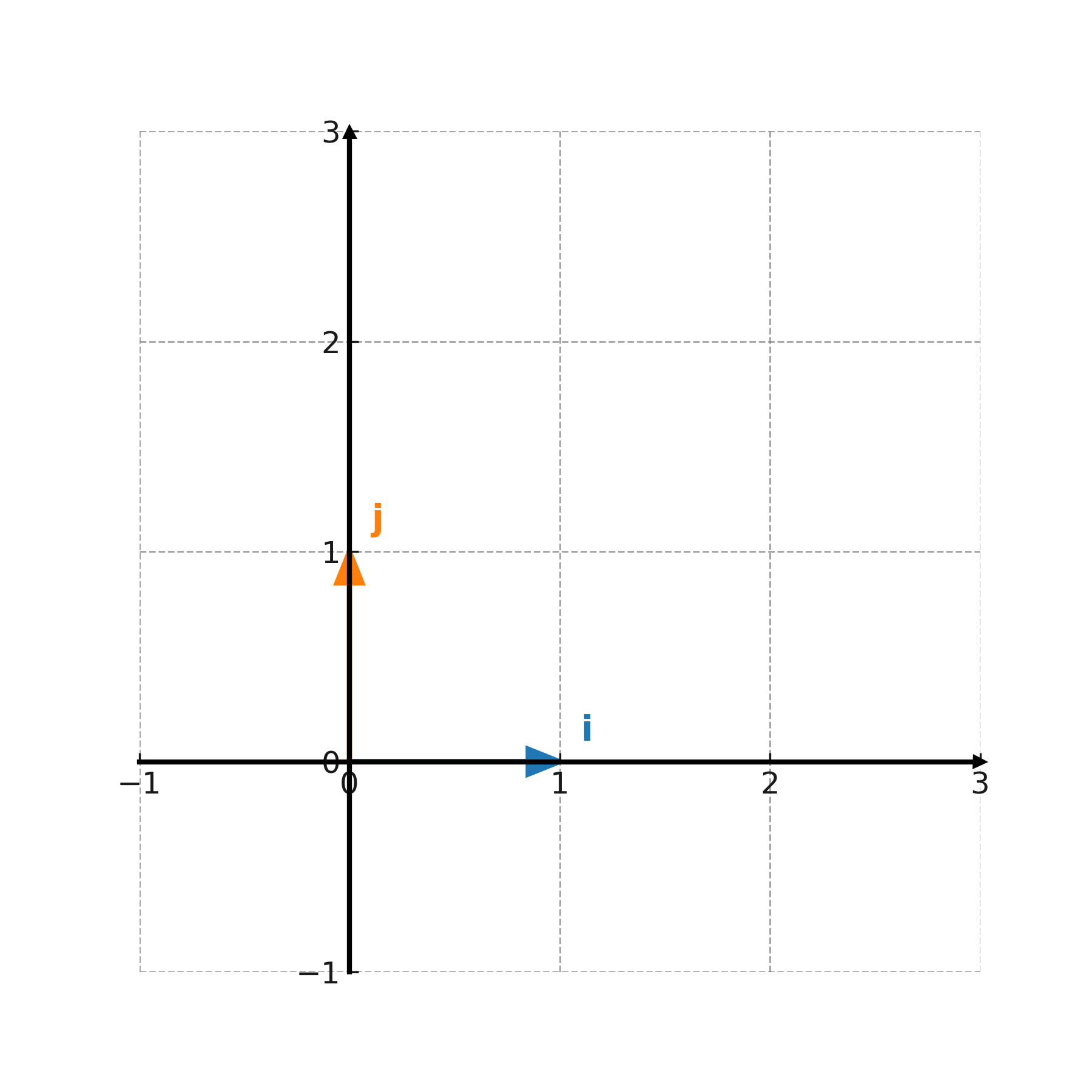
Dans un système de coordonnées, les vecteurs de base sont utilisés pour décrire tous les autres vecteurs. Dans le plan, la base standard est

 

$$ \large \mathbf{i} = (1,0), \quad \mathbf{j} = (0,1) $$

 

Chaque vecteur peut s’écrire comme une combinaison de ceux-ci : \( \large \mathbf{v} = x \cdot \mathbf{i} + y \cdot \mathbf{j} \).

 

Résumé

Les vecteurs directeurs servent à indiquer les directions de droites et de plans, les vecteurs normaux à indiquer les directions perpendiculaires, les vecteurs unitaires à isoler la direction pure, les vecteurs tangents à décrire l’évolution des courbes et les vecteurs de base à construire des systèmes de coordonnées entiers. Ensemble, ils constituent le fondement de l’utilisation des vecteurs en géométrie et en algèbre.