Addition et soustraction d’angles
En trigonométrie, l’addition et la soustraction des angles décrivent les formules qui montrent comment le sinus, le cosinus et la tangente changent lorsque deux angles sont additionnés ou soustraits.
Les formules permettent de calculer des valeurs pour de nouveaux angles à partir de valeurs connues.
Par exemple, on peut calculer cos(75°), même s’il n’apparaît pas dans les tables, en utilisant cos(45° + 30°).
Formules d’addition et de soustraction
Cosinus :
$$ \large \cos(\alpha + \beta) = \cos(\alpha) \cdot \cos(\beta) - \sin(\alpha) \cdot \sin(\beta) $$
$$ \large \cos(\alpha - \beta) = \cos(\alpha) \cdot \cos(\beta) + \sin(\alpha) \cdot \sin(\beta) $$
Sinus :
$$ \large \sin(\alpha + \beta) = \sin(\alpha) \cdot \cos(\beta) + \cos(\alpha) \cdot \sin(\beta) $$
$$ \large \sin(\alpha - \beta) = \sin(\alpha) \cdot \cos(\beta) - \cos(\alpha) \cdot \sin(\beta) $$
Tangente :
$$ \large \tan(\alpha + \beta) = \frac{\tan(\alpha) + \tan(\beta)}{1 - \tan(\alpha) \cdot \tan(\beta)} $$
$$ \large \tan(\alpha - \beta) = \frac{\tan(\alpha) - \tan(\beta)}{1 + \tan(\alpha) \cdot \tan(\beta)} $$
Exemple
Nous voulons calculer \( \cos(75^\circ) \). Cela peut s’écrire \( \cos(45^\circ + 30^\circ) \) :
$$ \large \cos(75^\circ) = \cos(45^\circ + 30^\circ) $$
$$ \large = \cos(45^\circ) \cdot \cos(30^\circ) - \sin(45^\circ) \cdot \sin(30^\circ) $$
$$ \large = \tfrac{\sqrt{2}}{2} \cdot \tfrac{\sqrt{3}}{2} - \tfrac{\sqrt{2}}{2} \cdot \tfrac{1}{2} $$
$$ \large = \tfrac{\sqrt{6}}{4} - \tfrac{\sqrt{2}}{4} = \tfrac{\sqrt{6} - \sqrt{2}}{4} $$
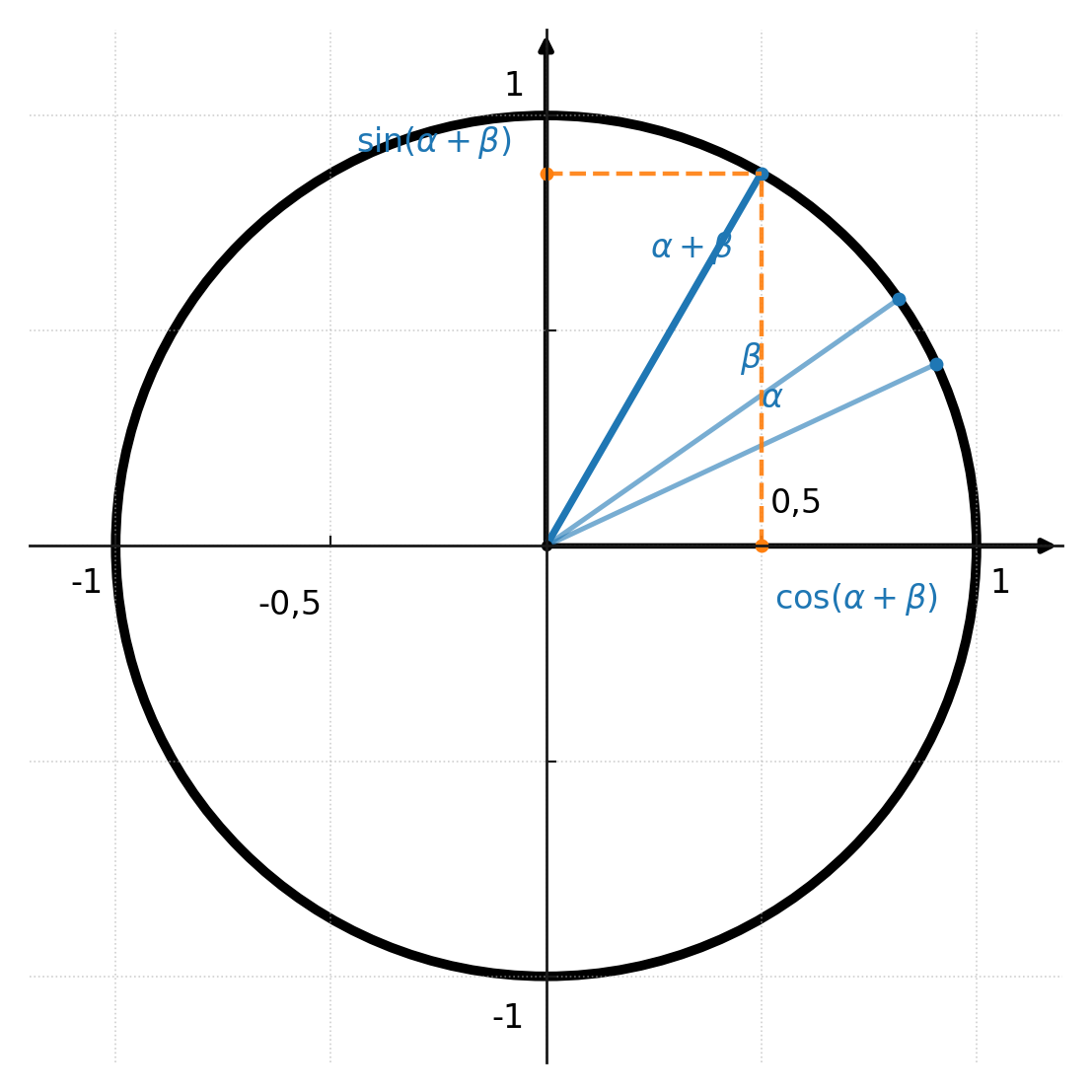
Les formules peuvent aussi être comprises géométriquement à partir du cercle unité.
Applications
- On peut calculer des valeurs exactes pour des angles comme 15°, 75° et 105°.
- Les formules sont à la base des formules de l’angle double et de l’angle moitié (en posant \( \alpha = \beta \)).
- Elles sont utilisées dans les démonstrations et les identités en trigonométrie avancée et en analyse.