Formules de l’angle double et demi-angle

En trigonométrie, les formules de l’angle double et demi angle décrivent comment le sinus, le cosinus et la tangente peuvent s’exprimer lorsque l’angle est doublé ou réduit de moitié.

Les formules dérivent directement des formules d’addition et de soustraction et permettent de trouver de nouvelles relations entre les fonctions trigonométriques.

 

Formules de l’angle double

En posant \( \alpha = \beta \) dans les formules d’addition, on obtient :

 

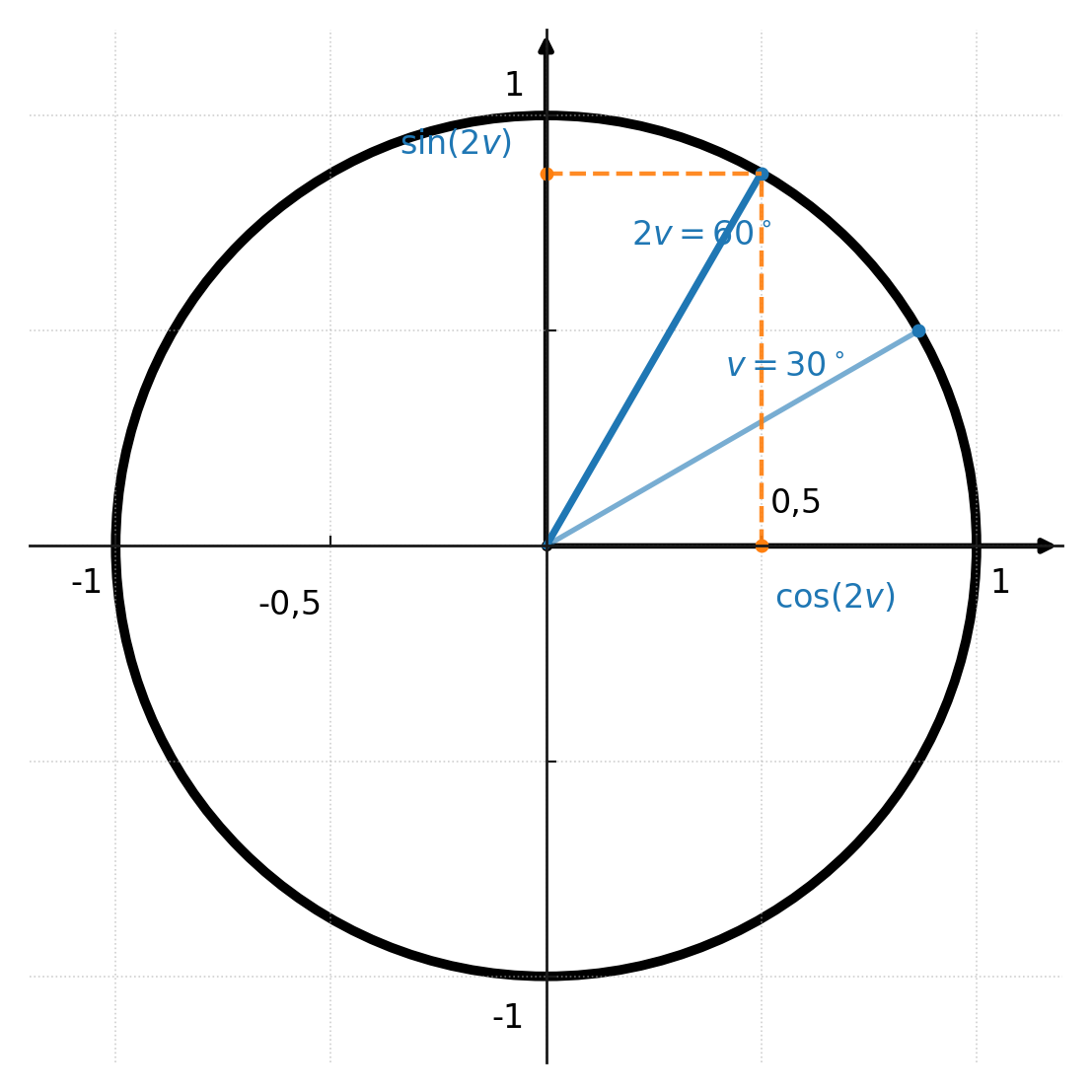
$$ \large \sin(2v) = 2 \sin(v) \cdot \cos(v) $$

$$ \large \cos(2v) = \cos^2(v) - \sin^2(v) $$

$$ \large \tan(2v) = \frac{2 \tan(v)}{1 - \tan^2(v)} $$

 

 

 

La formule du cosinus peut également être réécrite sous d’autres formes utiles à l’aide de l’identité de Pythagore :

 

$$ \large \cos(2v) = 2\cos^2(v) - 1 = 1 - 2\sin^2(v) $$

 

Formules du demi angle

Les formules du demi angle s’obtiennent en isolant \(\sin v\) et \(\cos v\) dans les formules de l’angle double. Le résultat est :

 

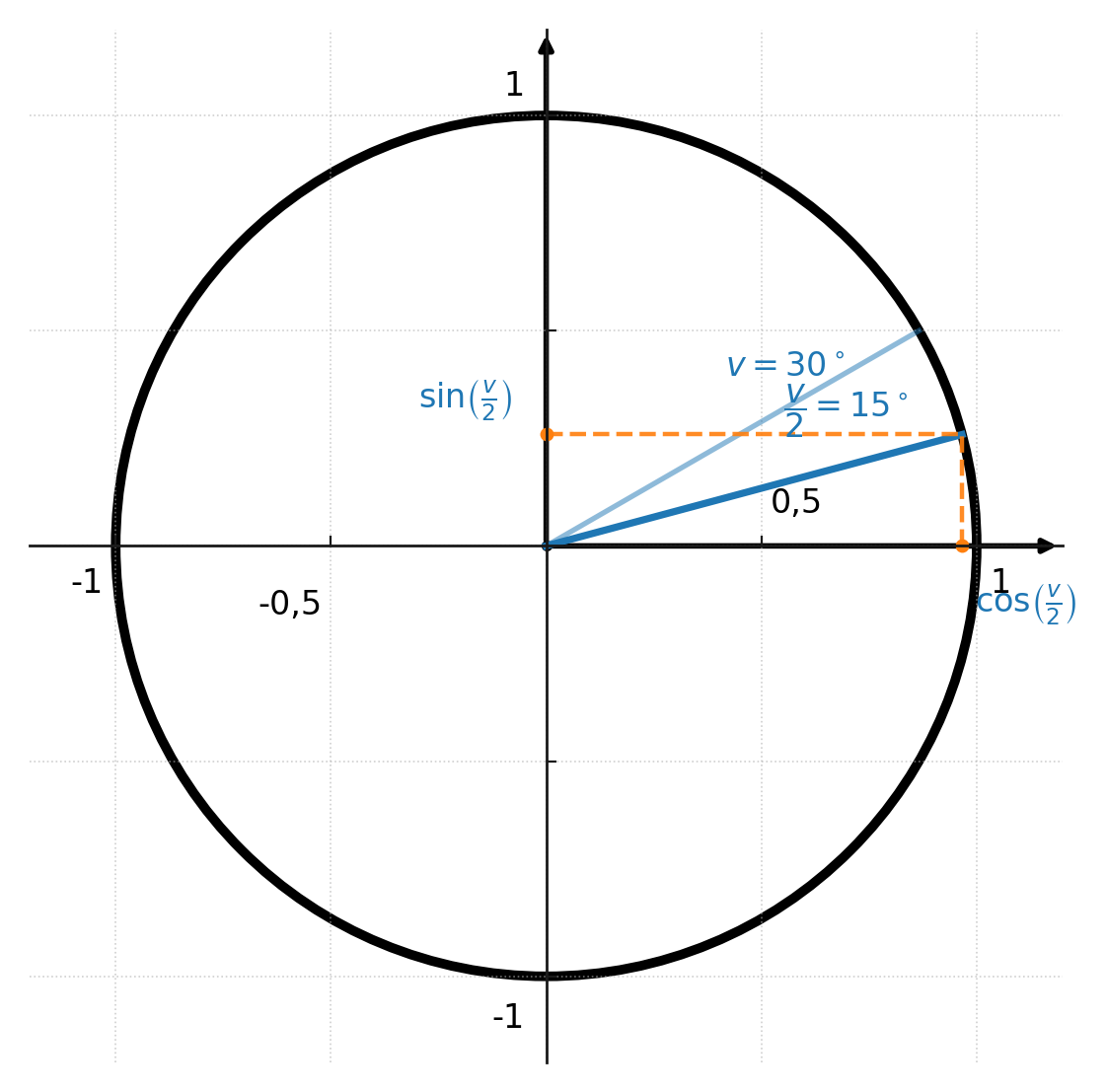
$$ \large \sin\!\left(\tfrac{v}{2}\right) = \pm \sqrt{\tfrac{1 - \cos(v)}{2}} $$

$$ \large \cos\!\left(\tfrac{v}{2}\right) = \pm \sqrt{\tfrac{1 + \cos(v)}{2}} $$

$$ \large \tan\!\left(\tfrac{v}{2}\right) = \tfrac{\sin(v)}{1 + \cos(v)} = \tfrac{1 - \cos(v)}{\sin(v)} $$

 

Les signes \(+\) ou \(-\) dépendent du quadrant dans lequel se trouve l’angle.

 

 

Exemple

Nous voulons calculer \( \sin(2 \cdot 30^\circ) \) :

 

$$ \large \sin(60^\circ) = 2 \cdot \sin(30^\circ) \cdot \cos(30^\circ) $$

$$  \large = 2 \cdot \tfrac{1}{2} \cdot \tfrac{\sqrt{3}}{2} = \tfrac{\sqrt{3}}{2} $$

 

Application

• Les formules servent à trouver des valeurs exactes pour des angles comme 15°, 22,5° et 75°.
• Elles sont utiles dans les démonstrations et les réécritures trigonométriques.
• Les formules du demi angle sont souvent utilisées pour résoudre des équations trigonométriques.