Fracciones impropias y números mixtos

Qué son las fracciones impropias

Una fracción se llama impropia cuando el numerador es mayor que el denominador. Por ejemplo: \(\large \frac{9}{8}\) 

 

Si recuerdas nuestra pizza, sabes que \(\large \frac{8}{8}\)  es igual a una pizza entera.

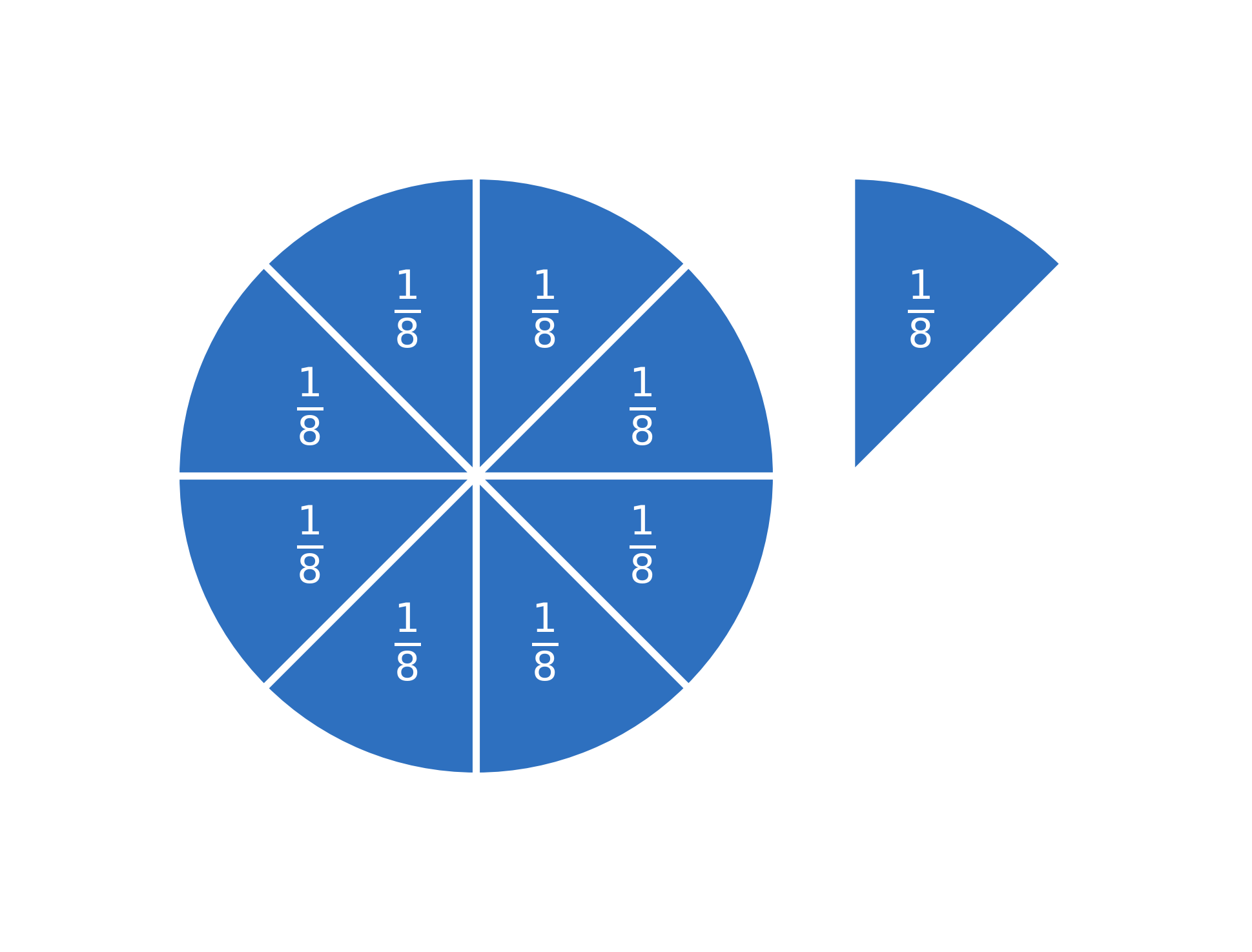
Esto significa que  \(\large \frac{9}{8}\)  es igual a una pizza entera + una porción extra, porque: 

 

$$ \large \frac{9}{8} \Leftrightarrow \frac{8}{8} + \frac{1}{8} $$

 

También se puede escribir así:

 

$$ \large 1+\frac{1}{8} = 1\frac{1}{8} $$

 

Otro ejemplo: \(\large \frac{15}{7}\) es una fracción impropia. Se puede escribir como \(\large 2\frac{1}{7}\)

 

 

Números mixtos

Cuando escribes \(\large 1+\frac{1}{8}\ \) puedes quitar el signo más, de modo que solo aparezca \(\large 1\frac{1}{8}\ \)

Esto se llama un número mixto, porque consta tanto de números enteros como de fracciones.

 

A menudo los números mixtos se reescriben como fracciones impropias al calcular:

$$ \large 2\frac{1}{7} = \frac{15}{7} $$

 

De hecho, es más fácil multiplicar y dividir fracciones impropias que números mixtos.

 

Puedes usar las mismas reglas de cálculo con fracciones impropias que con fracciones propias.

Solo debes recordar que no puedes dar una fracción impropia como resultado final en un ejercicio. Debe convertirse en un número mixto o un número entero.

 

 

Números enteros como fracciones

Todos los números enteros se pueden escribir como fracciones. Ya sabes que \(\large \frac{8}{8}=1\ \). Lo mismo se aplica a \(\large \frac{1}{1}=1\ \) 

 

Esto significa que \(\large 2=\frac{2}{1}\ \) 

 

La regla es así: \(\large a=\frac{a}{1}\ \) 

 

Pero también se puede escribir \(\large 4=\frac{8}{2}\ \). Esto es simplemente una ampliación de \(\large \frac{4}{1}\ \)  donde numerador y denominador se multiplican por 2. 

 

Una fracción también es una operación de división.

Dice: 8 dividido por 2 y eso es igual a 4.