Scale

Scale describes the relationship between a drawing and reality.

It can, for example, be a building plan or a map of a country. On the map or drawing, the scale will always be indicated, for example:

 

$$ \large 1 : 100 $$

 

This means that 1 cm on the drawing corresponds to 100 cm, that is, 1 meter, in reality.

It is always the case that the number on the left represents the drawing, and the number on the right represents reality.

Sometimes the ratio can be reversed, for example:

 

$$ \large 2 : 1 $$

 

Here the drawing is twice as large as reality. An enlarged scale can be used when drawing something very small in reality, for example an insect or a microchip.

 

 

Example

On a map of Denmark, the scale is:

 

$$ \large 1 : 500.000 $$

 

You need to find out how far it is from Roskilde to Copenhagen in reality.

On the map, you measure 6 cm.

 

 

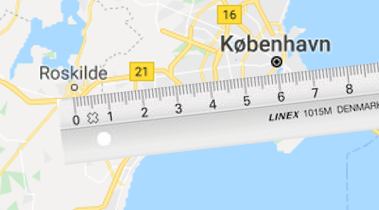
Each centimeter corresponds to 500,000 cm in reality. This means you must multiply by 6:

 

$$ \large 6 \cdot 500.000 = 3.000.000 \text{ cm} $$

 

So there are 3 million centimeters to Copenhagen. We want to convert that into kilometers.

There are 100,000 centimeters in one kilometer, so you must divide by 100,000:

 

$$ \large \frac{3.000.000}{100.000} = 30 \text{ km} $$

 

There are 30 kilometers from Roskilde to Copenhagen.