Dot product

The dot product is an operation between two vectors that produces a number. It is used to calculate angles between vectors and to determine whether they are perpendicular.

 

Definition

For two vectors in space \( \large \mathbf{u} = (x_1,y_1,z_1) \) and \( \large \mathbf{v} = (x_2,y_2,z_2) \), the dot product is defined as

 

$$ \large \mathbf{u} \cdot \mathbf{v} = x_1x_2 + y_1y_2 + z_1z_2 $$

 

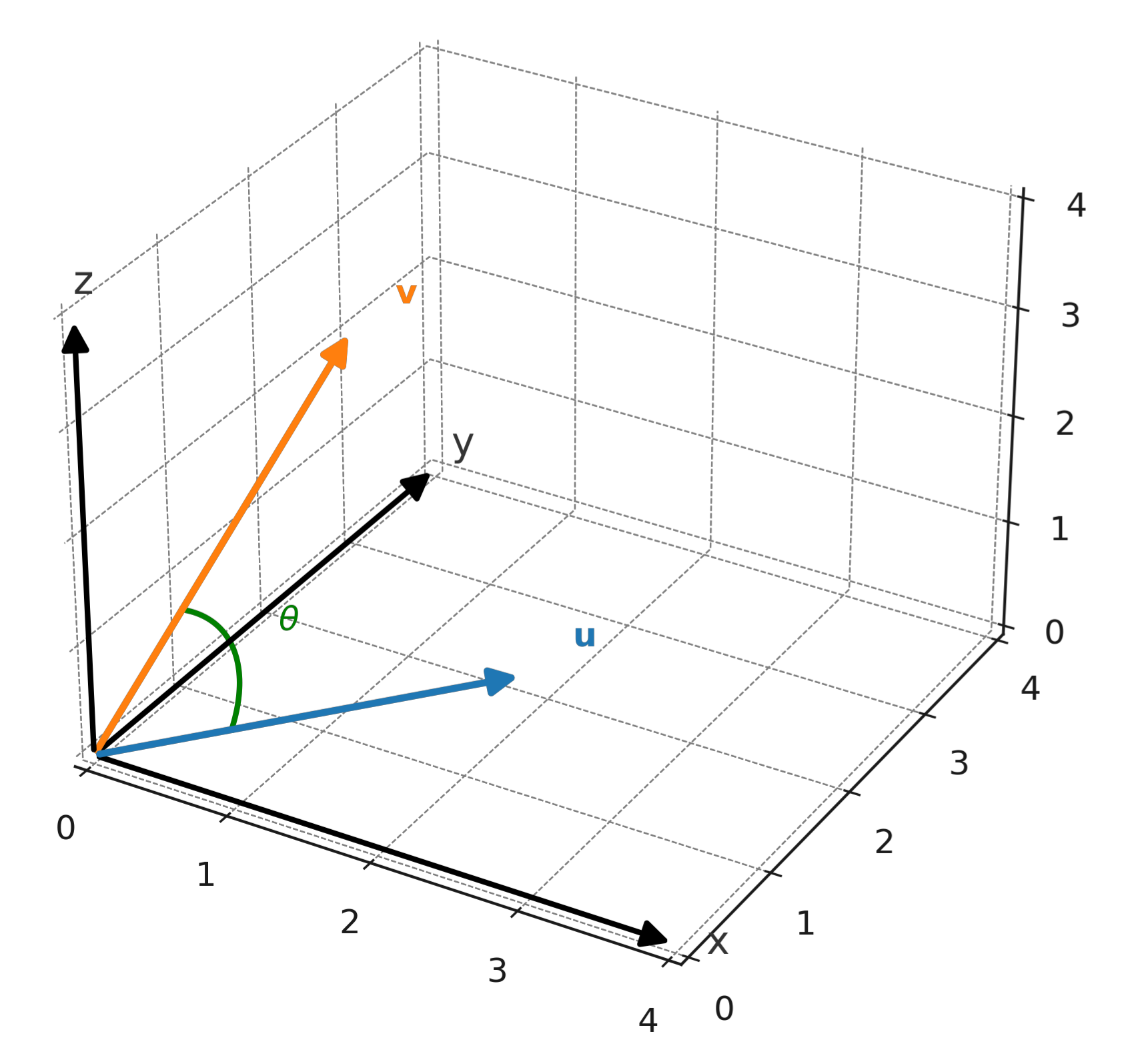
Another formula shows the relation with the angle between the vectors:

 

$$ \large \mathbf{u} \cdot \mathbf{v} = |\mathbf{u}| \cdot |\mathbf{v}| \cdot \cos(\theta) $$

 

where \( \large \theta \) is the angle between \( \large \mathbf{u} \) and \( \large \mathbf{v} \).

 

 

Example

We take \( \large \mathbf{u} = (1,2,3) \) and \( \large \mathbf{v} = (4,-1,2) \).

 

$$ \large \mathbf{u} \cdot \mathbf{v} = 1 \cdot 4 + 2 \cdot (-1) + 3 \cdot 2 = 4 - 2 + 6 = 8 $$

 

The dot product is 8.

 

 

Geometric interpretation

The dot product measures how much the two vectors point in the same direction. If the angle is less than 90°, the dot product is positive. If the angle is greater than 90°, the dot product is negative. If the vectors are perpendicular, the dot product is zero.

 

 

Application

The dot product is used in many contexts, including finding angles between vectors, determining orthogonality, and in physics to calculate work done by a force along a displacement.