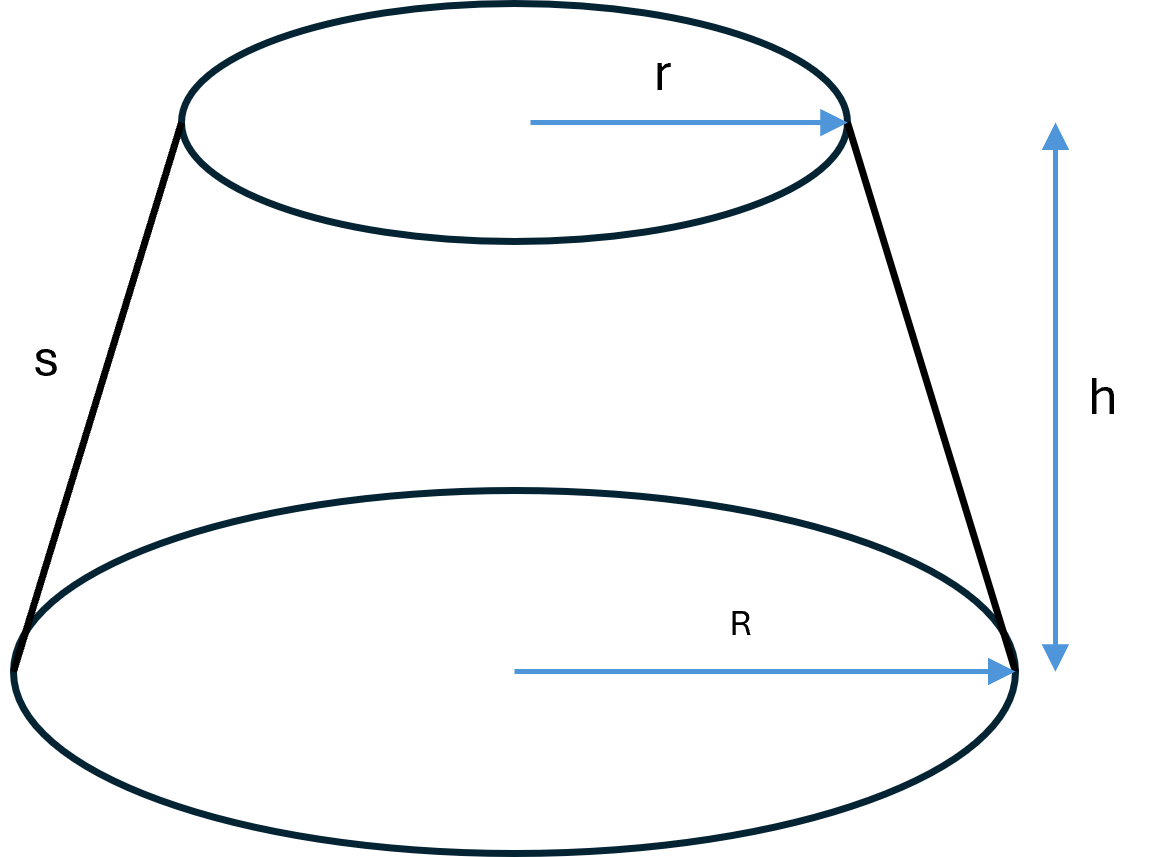
Cone frustum
A frustum of a cone is the spatial figure obtained when cutting off the top of a right cone with a plane parallel to the base.
The figure therefore has two parallel circular bases, one small and one large, as well as a curved lateral surface.
Volume
The volume of a frustum of a cone with large radius \( \large R \), small radius \( \large r \) and height \( \large h \) is:
$$ V = \frac{1}{3} \cdot \pi \cdot h \cdot \left(R^2 + R \cdot r + r^2\right) $$
Surface area
The surface area consists of the two circular bases and the curved lateral surface. The area of the lateral surface is calculated from the slant height \( \large s \):
$$ S = \pi \cdot R^2 + \pi \cdot r^2 + \pi \cdot (R + r) \cdot s $$
where the slant height is found by:
$$ s = \sqrt{h^2 + (R-r)^2} $$
Oblique cone frustum
An oblique cone frustum is obtained when cutting an oblique cone with a plane parallel to the base.
The figure therefore has two parallel circular bases, but the centers of the two circles are displaced, and the lateral surface is slanted.
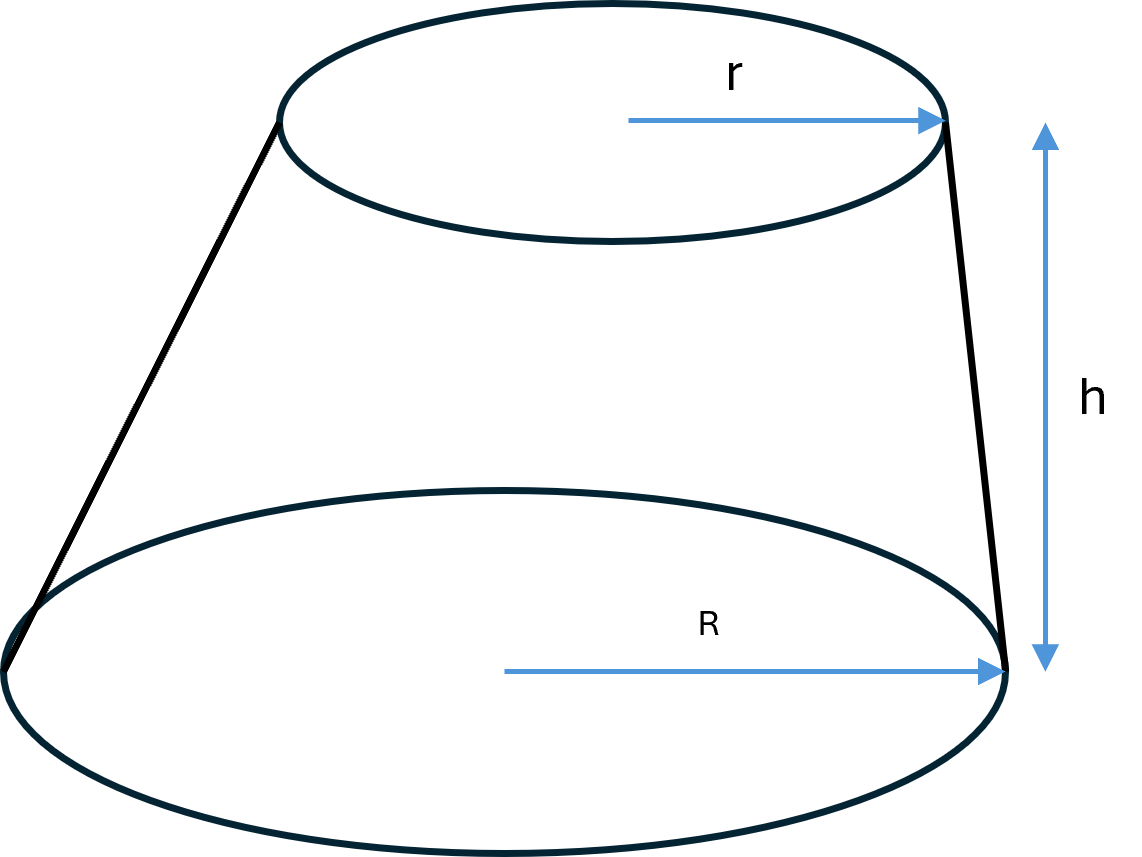
The volume can still be calculated with the same formula as for the right cone frustum:
$$ V = \frac{1}{3} \cdot \pi \cdot h \cdot \left(R^2 + R \cdot r + r^2\right) $$
The surface area, however, becomes more complicated, because the curved lateral surface can no longer be described by a single slant height. One typically has to use integral calculus or divide the surface into smaller parts to calculate it precisely.
Truncated cone
If a cone is cut by a plane that is not parallel to the base, one obtains a truncated cone. In this case the top surface is no longer a circle but an ellipse.
One can distinguish between two types of truncated cones:
Right truncated cone:
The starting point is a right cone. The cut surface is an ellipse, and the figure is symmetric about the axis of the cone.
Oblique truncated cone:
The starting point is an oblique cone. The cut surface is also an ellipse, but the figure is not symmetric.

Truncated cones are much more difficult to calculate, because the lateral surface is no longer a regular cone surface.
Volume and surface area can be found using integral calculus, but there are no simple closed formulas as for the ordinary cone frustums.