Set operations are methods to combine or compare sets. Here we look at unions, intersections, disjoint sets, differences, complements, and how these can be visualized with Venn diagrams.

 

Union

The union of two sets \( \large A\) and \( \large B\) is the set of all elements that are in either \( \large A\) or \( \large B\) (or both). It is written as:

 

$$ \large A \cup B = \{x \mid x \in A \;\vee\; x \in B\} $$

 

Example: If \( \large A = \{1,2,3\}\) and \( \large B = \{3,4,5\}\), then \( \large A \cup B = \{1,2,3,4,5\}\).

 

 

 

 

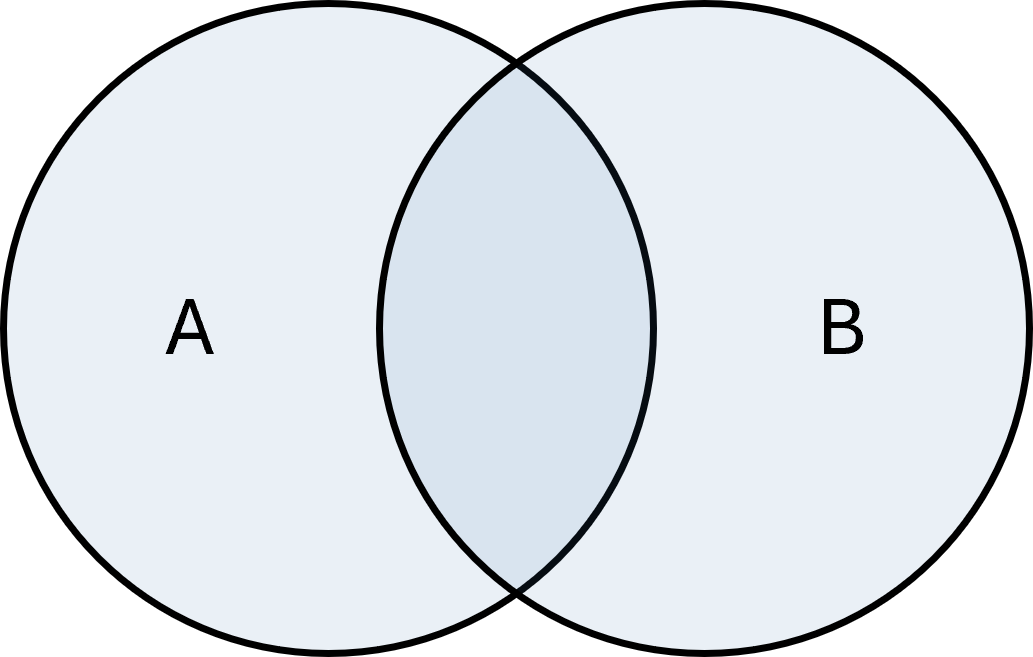
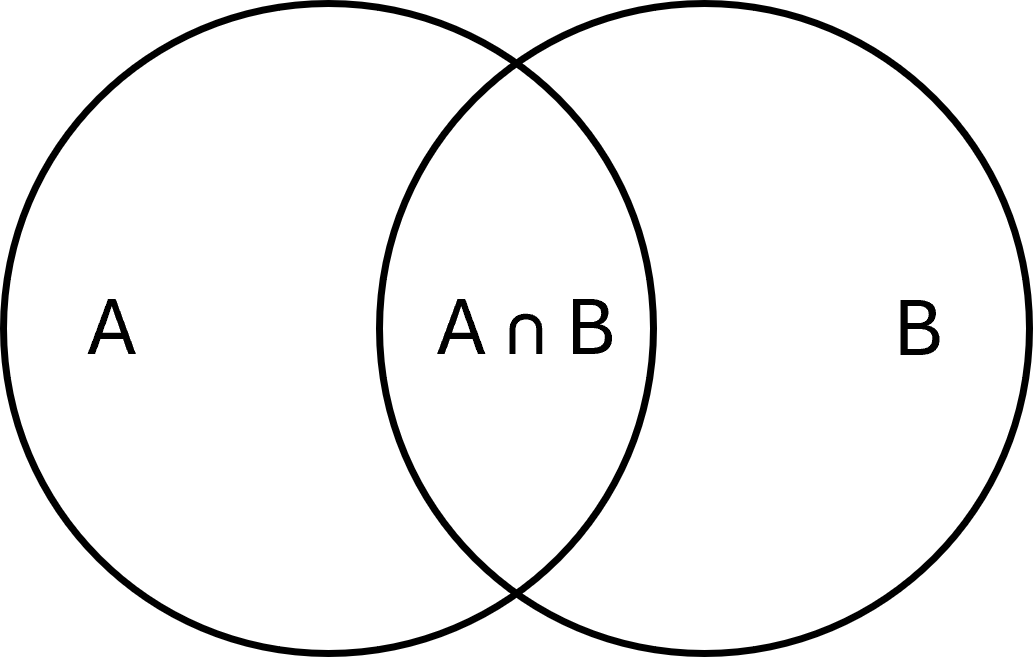
Intersection

The intersection of two sets is the elements they have in common. It is written as:

 

$$ \large A \cap B = \{x \mid x \in A \;\wedge\; x \in B\} $$

 

Example: If \( \large A = \{1,2,3\}\) and \( \large B = \{3,4,5\}\), then \( \large A \cap B = \{3\}\).

 

 

 

 

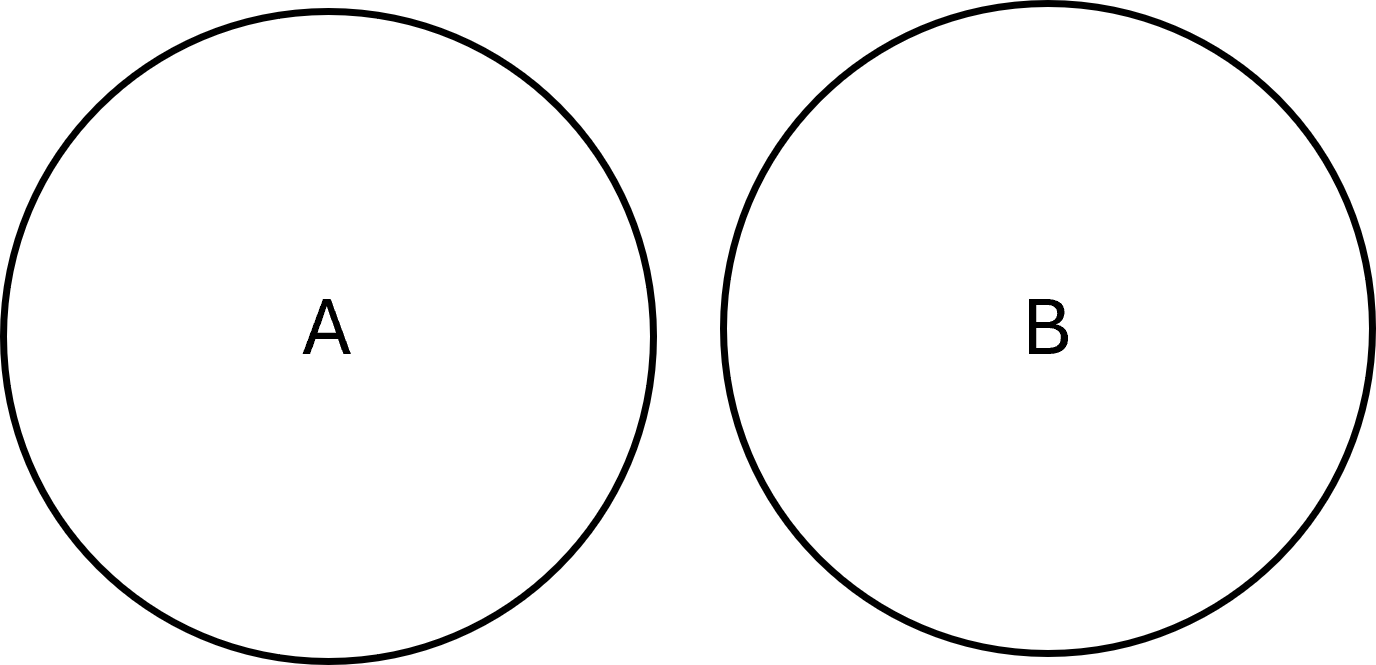
Disjoint sets

Two sets are disjoint if they have no elements in common. That is, their intersection is empty:

 

$$ \large A \cap B = \emptyset $$

 

Example: \( \large A = \{1,2,3\}, B = \{4,5,6\}\).

 

 

 

 

Difference

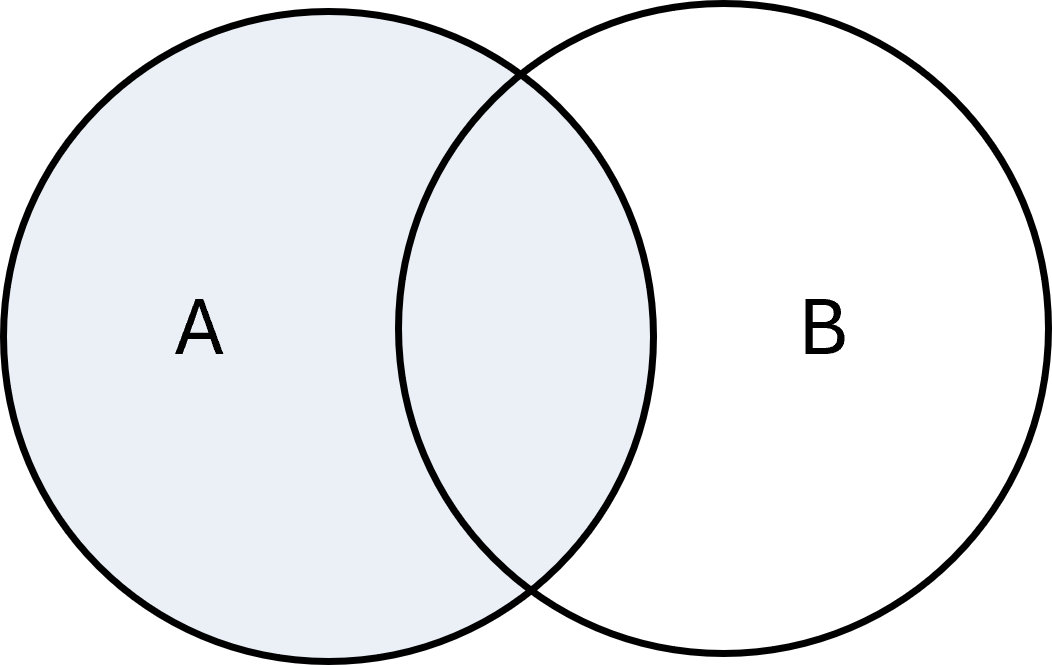
The difference of two sets \( \large A\) and \( \large B\), written as \( \large A - B\) or \( \large A \setminus B\), is the elements that are in \( \large A\) but not in \( \large B\):

 

$$ \large A - B = \{x \mid x \in A \;\wedge\; x \notin B\} $$

 

Example: If \( \large A = \{1,2,3\}, B = \{3,4,5\}\), then \( \large A - B = \{1,2\}\).

 

 

 

 

Complement

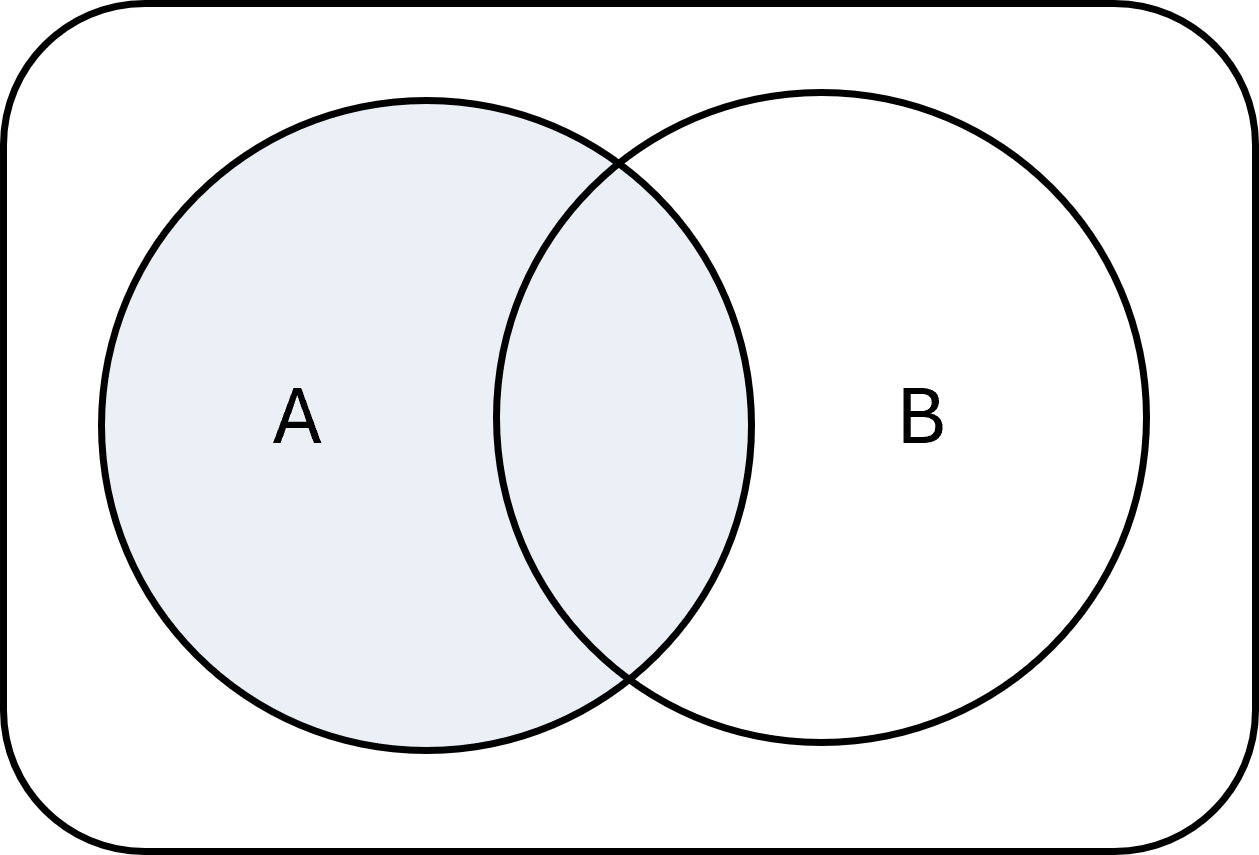
If we have a universe \( \large U\) that contains all possible elements, we can define the complement of a set \( \large A\) as all the elements in \( \large U\) that are not in \( \large A\). It is written as:

 

$$ \large A^{c} = \{x \in U \mid x \notin A\} $$

 

Example: If \( \large U = \{1,2,3,4,5\}\) and \( \large A = \{1,2\}\), then \( \large A^{c} = \{3,4,5\}\).

 

 

 

 

Venn diagrams

Venn diagrams are often used to illustrate set operations graphically.

Circles represent sets, and overlapping areas show how union, intersection, difference, and complement work.