Injective, Surjective and Bijective Functions

In mathematics, functions can have different properties depending on how the elements in the domain and codomain are connected.

The three most important are injective, surjective and bijective.

Injective function

A function $ \large f : A \to B$ is injective if two different elements in $ \large A$ always get different images in $ \large B$.

In other words:

$$ \large f(a_1) = f(a_2) \;\Rightarrow\; a_1 = a_2 $$

Example:

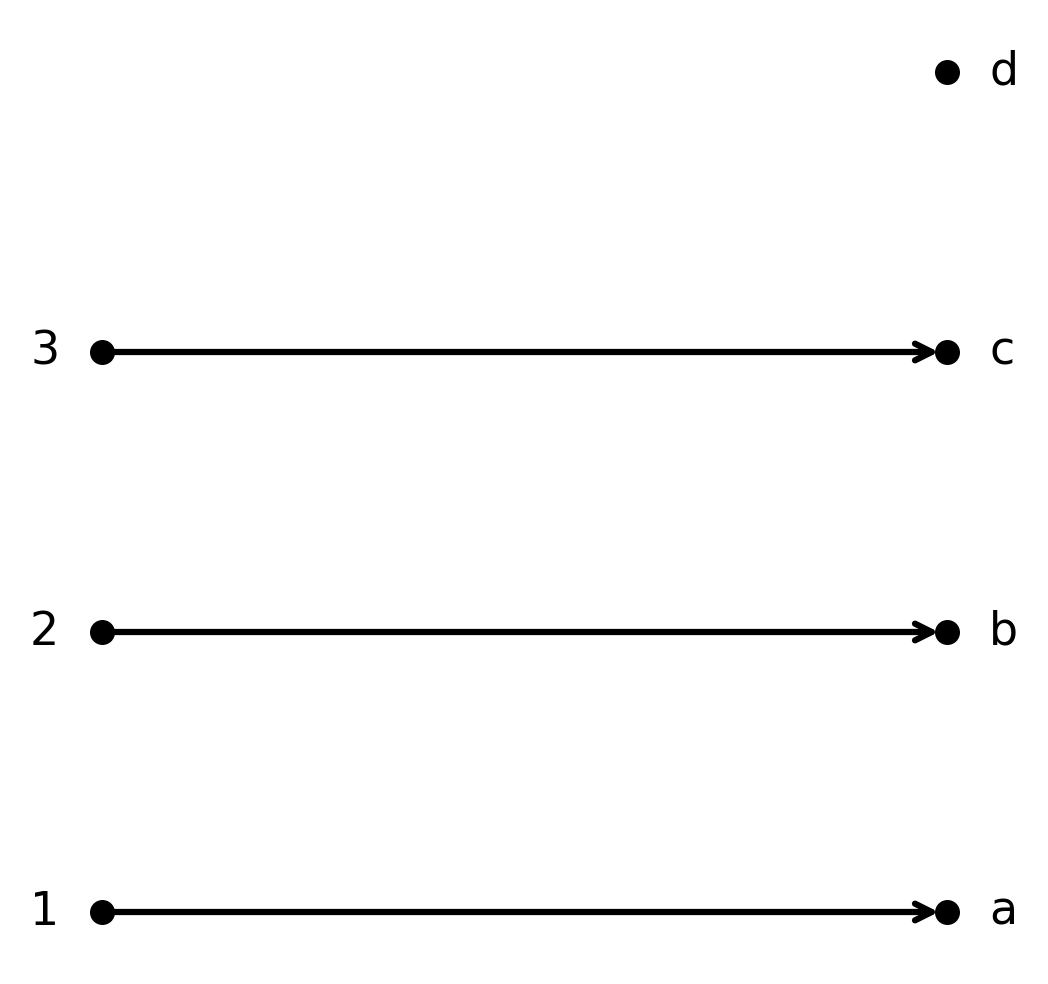
The function $ \large f : \{1,2,3\} \to \{a,b,c,d\}$ given by $ \large f(1)=a, f(2)=b, f(3)=c$ is injective.

Each element in $ \large A$ maps to a unique element in $ \large B$, but not the whole codomain is covered.

Injective function

Surjective function

A function $ \large f : A \to B$ is surjective if every element in $ \large B$ is hit by at least one element from $ \large A$.

That is:

$$ \large \forall b \in B, \;\exists a \in A : f(a) = b $$

Example:

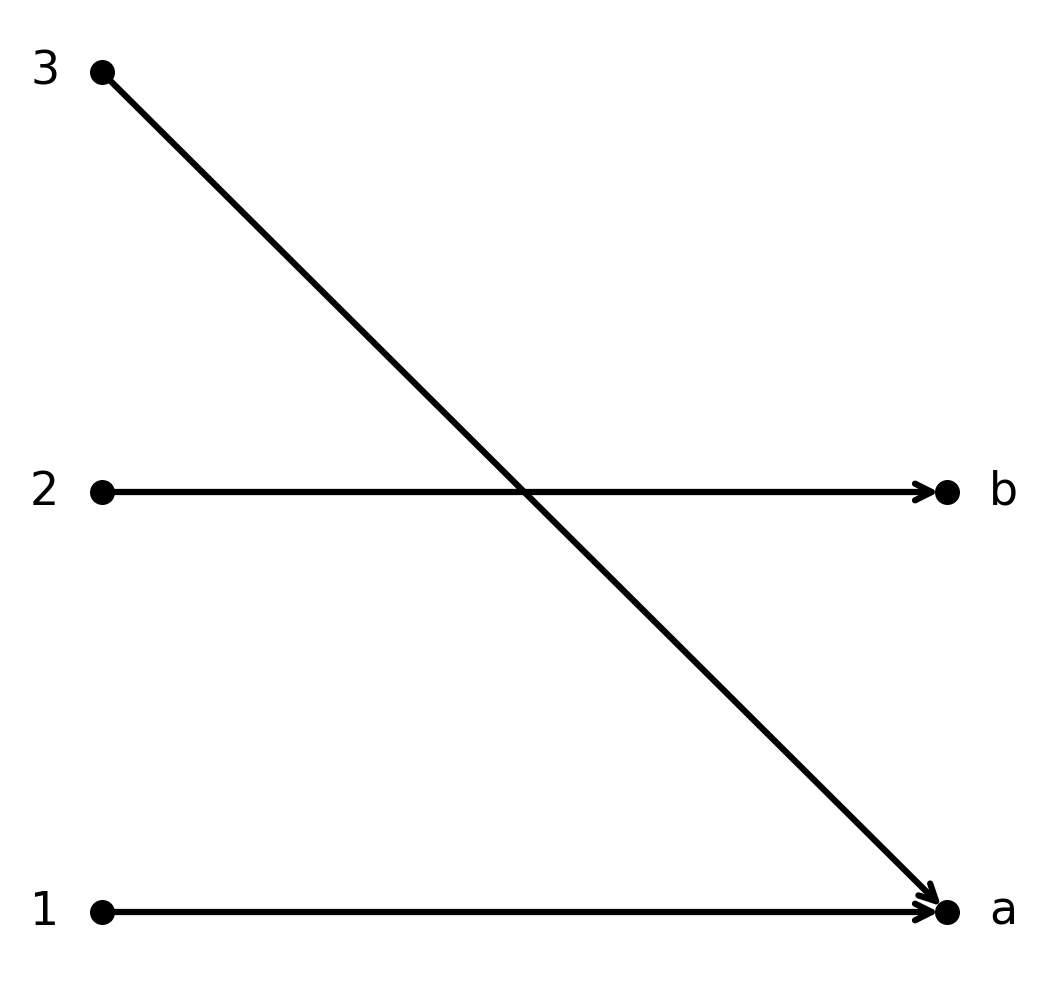
The function $ \large f : \{1,2,3\} \to \{a,b\}$ given by $ \large f(1)=a, f(2)=b, f(3)=a$ is surjective.

Both elements in $ \large B$ are hit, but the function is not injective, since $ \large 1$ and $ \large 3$ both map to $ \large a$.

Surjective function

Bijective function

A function is bijective if it is both injective and surjective.

This means that there is a one-to-one correspondence between the elements of $ \large A$ and $ \large B$. Each element in $ \large A$ maps to a unique element in $ \large B$, and the whole $ \large B$ is covered.

Example:

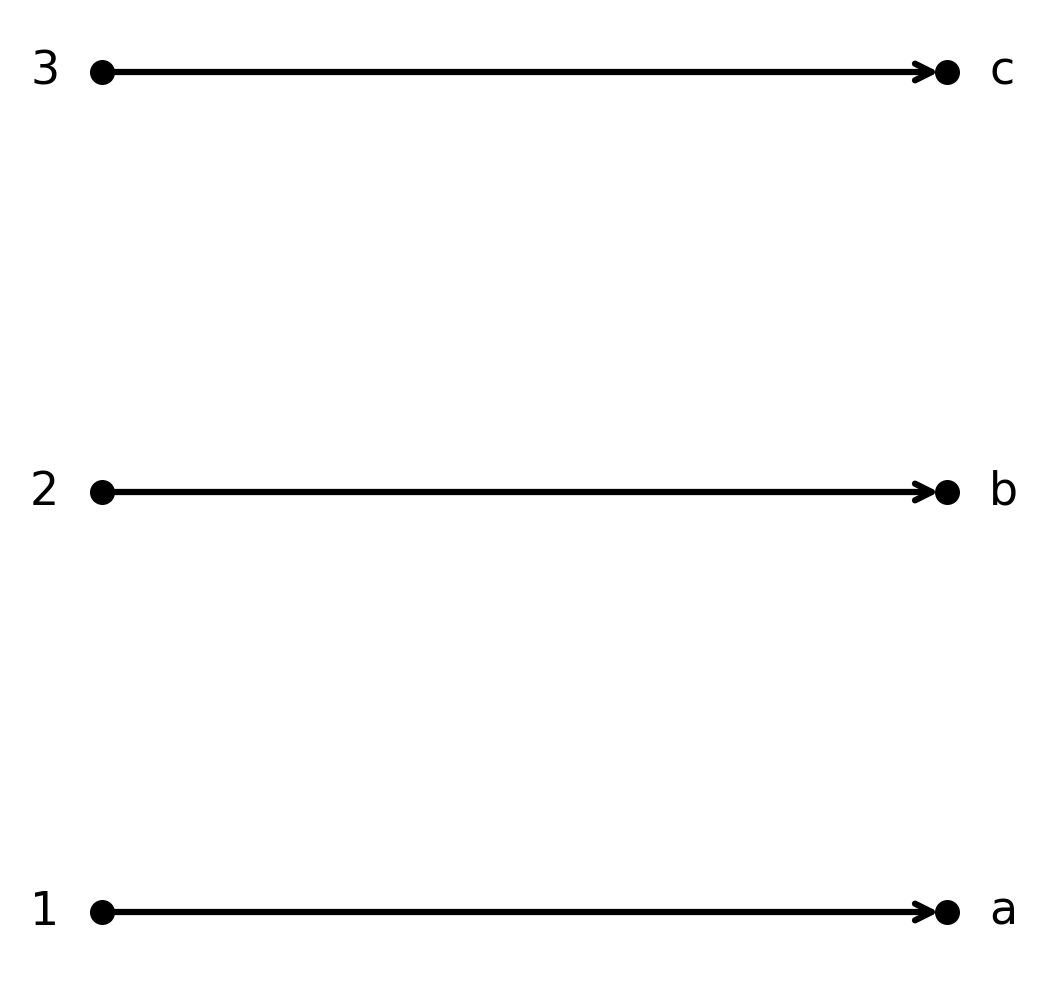
The function $ \large f : \{1,2,3\} \to \{a,b,c\}$ given by $ \large f(1)=a, f(2)=b, f(3)=c$ is bijective.

Each element in $ \large A$ is paired with a unique element in $ \large B$, and all elements in $ \large B$ are hit.

Bijective function

Summary

Injective: Two different inputs always give different outputs.
Surjective: The entire codomain is covered.
Bijective: Combination of the two – there exists a one-to-one correspondence, which can be reversed.

Bijective functions are especially important because they always have an inverse function, making it possible to go back from output to input.