Cartesian Product in Two and Higher Dimensions

The Cartesian product is a way of combining sets to form ordered pairs or tuples. The name comes from the French mathematician René Descartes (Latin: Cartesius), because the concept forms the basis of coordinate systems and the geometric representation of points.

 

 

Cartesian product of two sets

If we have two sets \( \large A\) and \( \large B\), their Cartesian product is the set of all ordered pairs where the first element comes from \( \large A\) and the second element from \( \large B\):

 

$$ \large A \times B = \{(a,b) \mid a \in A, \; b \in B\} $$

 

Example: Let \( \large A = \{1,2\}\) and \( \large B = \{x,y\}\). Then:

 

$$ \large A \times B = \{(1,x), (1,y), (2,x), (2,y)\} $$

 

 

 

 

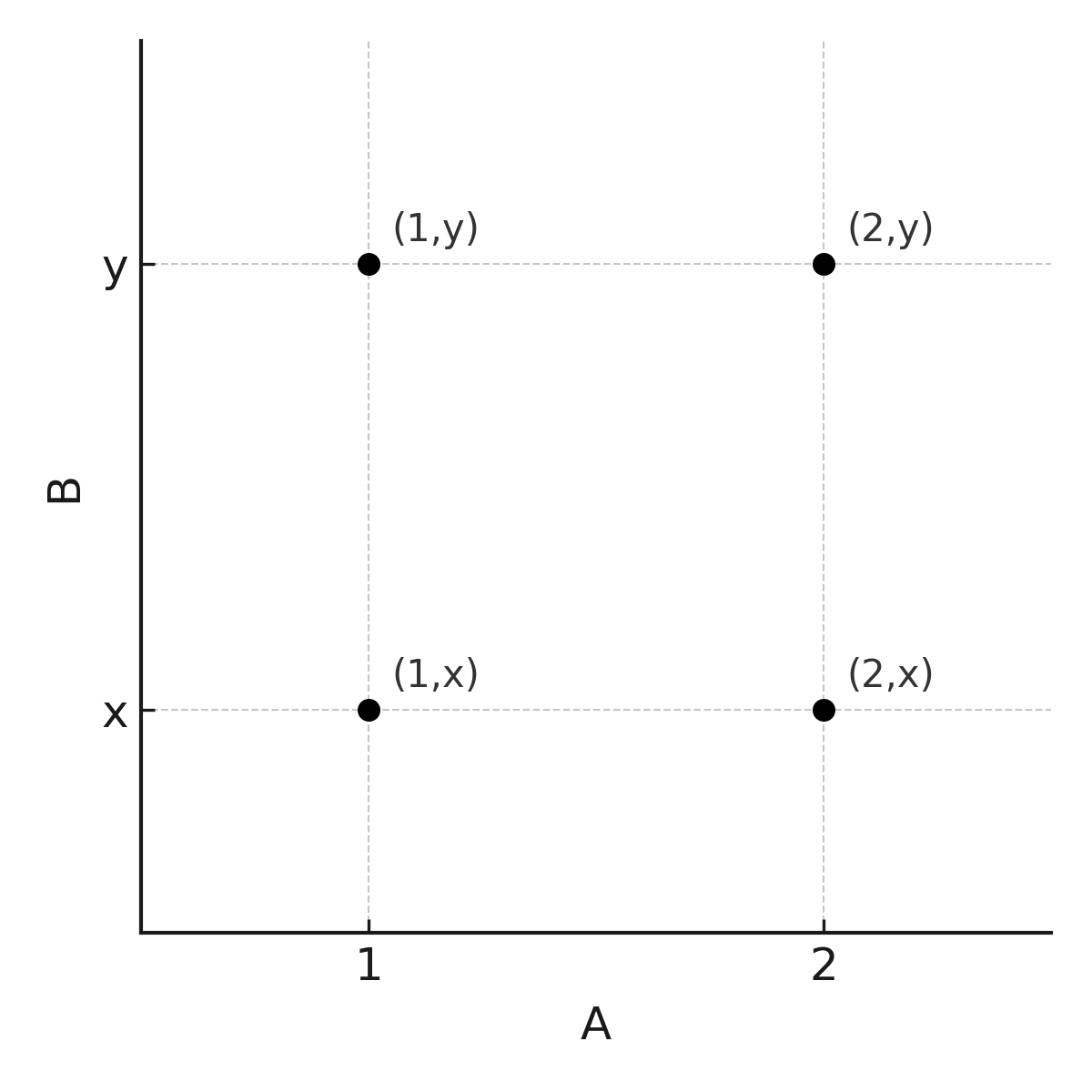
Note: Order matters. The set \( \large B \times A\) is:

 

$$ \large B \times A = \{(x,1),(x,2),(y,1),(y,2)\} $$

 

So in general: \( \large A \times B \neq B \times A\).

 

The cardinality (number of elements) of the product is given by:

 

$$ \large |A \times B| = |A| \cdot |B| $$

 

Example: If \( \large |A|=3\) and \( \large |B|=4\), then \( \large A \times B\) contains \( \large 3 \cdot 4 = 12\) ordered pairs.

 

 

Cartesian product in higher dimensions

The idea can be extended to three or more sets. For three sets it is defined as:

 

$$ \large A \times B \times C = \{(a,b,c) \mid a \in A, \; b \in B, \; c \in C\} $$

 

Example: If \( \large A = \{1,2\}, B = \{x\}, C = \{p,q\}\), then:

 

$$ \large A \times B \times C = \{(1,x,p), (1,x,q), (2,x,p), (2,x,q)\} $$

 

In general, one can define a Cartesian product of \( \large n\) sets, which contains all \( \large n\)-tuples where each element comes from one of the sets. If all the sets are the same, for example \( \large A \times A \times \cdots \times A\) (with \( \large n\) repetitions), this is written as \( \large A^n\).

 

Examples:

 

• \( \large \mathbb{R}^2\): all points in the plane, written as \((x,y)\).
• \( \large \mathbb{R}^3\): all points in space, written as \((x,y,z)\).
• \( \large \{0,1\}^3\): all binary triples, i.e. \( \large (0,0,0),(0,0,1),\ldots,(1,1,1)\).

 

The number of elements in a Cartesian product of finite sets is:

 

$$ \large |A_1 \times A_2 \times \cdots \times A_n| = |A_1| \cdot |A_2| \cdot \ldots \cdot |A_n| $$

 

 

Significance and applications

Cartesian products provide a systematic way to build new structures from known sets.

They are the foundation for:

 

• Coordinate systems in mathematics and geometry.
• Tables and data structures in computer science.
• Relations between objects (e.g. graphs).