Improper fractions and mixed numbers

What are improper fractions

A fraction is called improper when the numerator is larger than the denominator. For example: \(\large \frac{9}{8}\) 

 

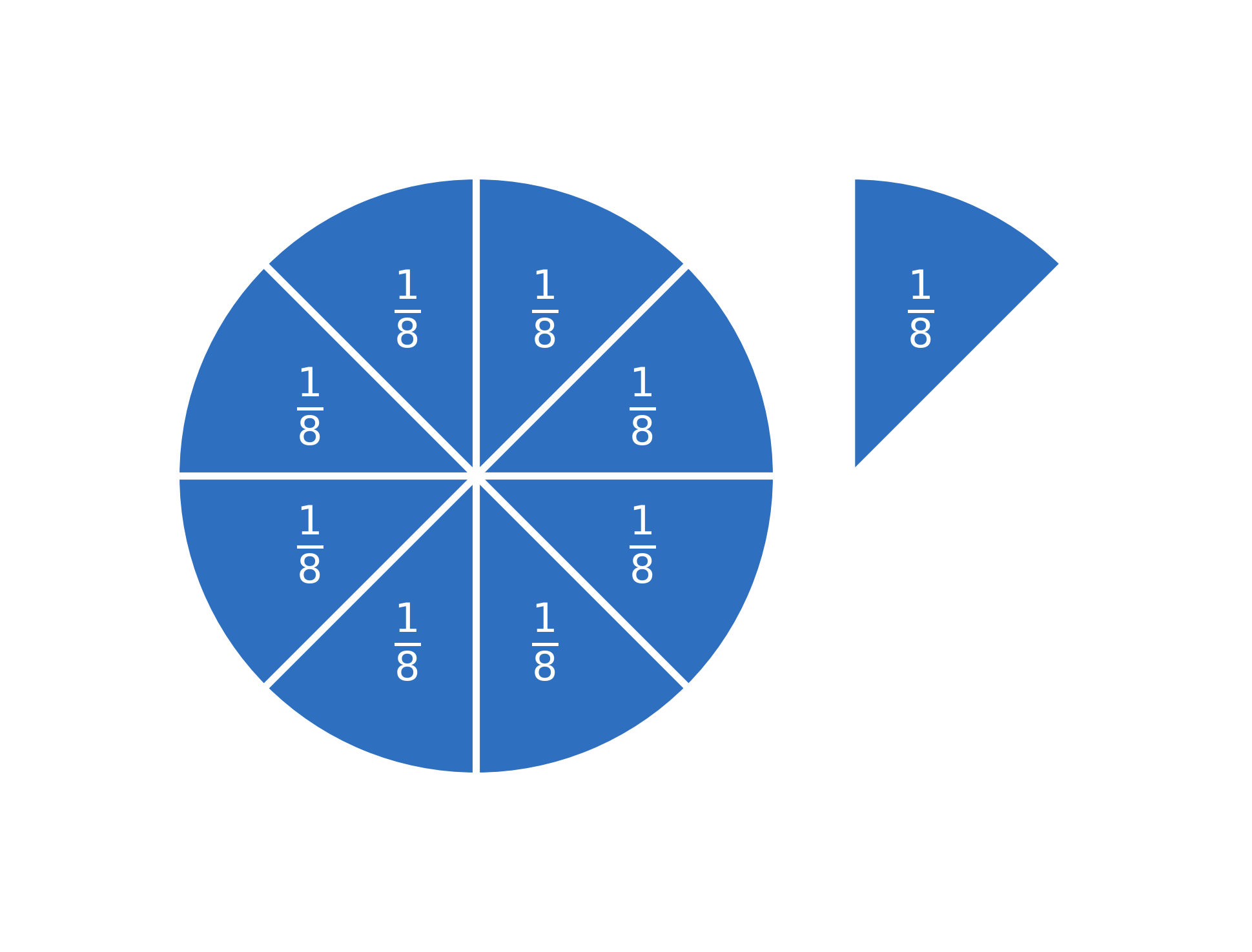
If you remember our pizza, you know that \(\large \frac{8}{8}\)  is equal to a whole pizza.

This means that  \(\large \frac{9}{8}\)  is equal to a whole pizza + one extra slice, because: 

 

$$ \large \frac{9}{8} \Leftrightarrow \frac{8}{8} + \frac{1}{8} $$

 

It can also be written like this:

 

$$ \large 1+\frac{1}{8}  = 1\frac{1}{8} $$

 

Another example: \(\large \frac{15}{7}\) is an improper fraction. It can be written as \(\large 2\frac{1}{7}\)

 

 

Mixed numbers

When you write \(\large 1+\frac{1}{8}\ \) you can remove the plus sign, so it just says \(\large 1\frac{1}{8}\ \)

This is called a mixed number, because it consists of both whole numbers and fractions.

 

Mixed numbers are often rewritten as improper fractions when calculating:

$$ \large 2\frac{1}{7} = \frac{15}{7} $$

 

It is in fact easier to multiply and divide improper fractions than mixed numbers.

 

You can use the same calculation rules on improper fractions as you use on proper fractions.

You just have to remember that you cannot give an improper fraction as the final answer in a problem. It must be converted into a mixed number or a whole number.

 

 

Whole numbers as fractions

All whole numbers can be written as fractions. You already know that \(\large \frac{8}{8}=1\ \). The same applies to \(\large \frac{1}{1}=1\ \) 

 

This means that \(\large 2=\frac{2}{1}\ \) 

 

The rule is like this: \(\large a=\frac{a}{1}\ \) 

 

But you can also write \(\large 4=\frac{8}{2}\ \). This is simply an expansion of \(\large \frac{4}{1}\ \)  where numerator and denominator are multiplied by 2. 

 

A fraction is also a division problem.

It says: 8 divided by 2 and that is equal to 4.