Polygoner

En polygon er en "mangekant", altså en figur med mange kanter.

Hvad er så "mange kanter"?

Det dækker over alle figurer med kanter, også trekanter og firkanter. Dem har vi givet særskilte navne, i stedet for blot at sige "en polygon med tre kanter".

Så polygon er en fælles betegnelse for figurer med flere kanter.

Forskellige polygoner

Polygoner kan enten være konvekse eller konkave og regulære eller irregulære:

	Konveks	Konkav
Regulær	Alle vinkler er under 180^o Alle sider er ens	En eller flere vinkler er over 180^o Alle sider er ens
Irregulær	Alle vinkler er under 180^o Sider er ikke ens	En eller flere vinkler er over 180^o Sider er ikke ens

Figurer

Her er de fire typer vist som figurer:

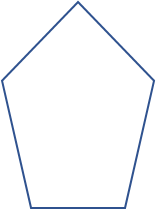
	Konveks	Konkav
Regulær
Irregulær

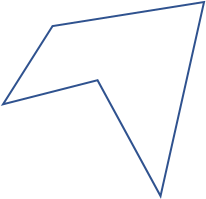Kompleks polygon

De fire ovenstående kaldes alle for simple polygoner og herudover er der komplekse polygoner, hvor linjerne også krydser hinanden.

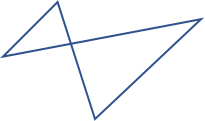
Kompleks polygon

Vinkelsum i polygoner

Vinkelsummen i en polygon kan regnes med flg. formel:

$$ Vinkelsum = (Antal\ kanter - 2) \cdot 180 \\[12pt] \Leftrightarrow \\[12pt] \sum \alpha = (n-2)\cdot 180 $$

Hvis du bruger denne formel på konkave polygoner, skal du huske at den beregner den indvendige vinkelsum.

Areal

For regulære konvekse polygoner er der en formel, der kan regne arealet ud:

$$ Areal=\frac{1}{4} \cdot n \cdot b^2 \cdot cot \biggl( \frac{\pi}{n} \biggr) $$

Hvor $n$ = Antal kanter og $b$ = sidelængde.

Hvis du har en 5-kant, med en sidelængde på 8, ville det se sådan her ud:

$$ Areal=\frac{1}{4} \cdot 5 \cdot 8^2 \cdot cot \biggl( \frac{\pi}{5} \biggr) \Leftrightarrow $$

$$ Areal=\frac{5 \cdot 64 \cdot 1,376382}{4} \Leftrightarrow $$

$$ Areal = 110,11 $$

Cot er CoTangens (Cosinus divideret med Sinus). Hvis din lommeregner ikke har den knap, kan du regne det ud sådan her:

$$ cot \biggl( \frac{\pi}{n} \biggr)= \frac{cos \biggl( \frac{\pi}{n} \biggr)}{sin \biggl( \frac{\pi}{n} \biggr)} $$

Omkreds

Omkredsen er der ikke særlige regler for. Der er kun at finde sidelængder og lægge dem sammen.

I det hele taget, når du regner på polygoner og der ikke findes en formel, går det ud på at få figuren delt op i nogle figurer, som du kan regne på.

Her er det godt at have overblik over trigonometri.

Pentagram

En kendt kompleks polygon, som de fleste nemt kan tegne er et Pentagram.

Det kan tegnes i en streg uden at løfte blyanten.

Pentagram

Pentagrammet er en kompleks polygon, fordi stregerne krydser hinanden.

Det viste pentagram er samtidigt regulært, fordi alle sider er lige lange.

Dekagon (Ti-kant)

Dekagonet herunder er ikke en kompleks polygon. Den er en konkav regulær polygon.

Dekagon

Den vil også kunne tegnes irregulært. Ti-kantens indvendige vinkelsum er 1440^o

Navne på polygoner

Antal kanter	Navn	Vinkelsum
3	Trigon	180^o
4	Tetragon	360^o
5	Pentagon	540^o
6	Heksagon	720^o
7	Heptagon	900^o
8	Oktagon	1.080^o
9	Novegon	1.260^o
10	Dekagon	1.440^o
11	Hendekagon	1.620^o
12	Dodekagon	1.800^o
13	Tridekagon	1.980^o
14	Tetradekagon	2.160^o
15	Pentadekagon	2.340^o
16	Heksadekagon	2.520^o
17	Heptadekagon	2.700^o
18	Oktadekagon	2.880^o
19	Enneadecagon	3.060^o
20	Icosagon	3.240^o
50	Pentacontagon	8.640^o
1.000	Chiliagon	179.640^o
10.000	Myriagon	1.799.640^o