Polygones

Un polygone est une "figure à plusieurs côtés", c’est-à-dire une figure avec de nombreux côtés.

Que signifie alors "plusieurs côtés" ?

Cela englobe toutes les figures avec des côtés, y compris les triangles et les quadrilatères. Nous leur avons donné des noms distincts au lieu de dire simplement "un polygone à trois côtés".

Ainsi, polygone est un terme général pour les figures avec plusieurs côtés.

Différents polygones

Les polygones peuvent être convexes ou concaves et réguliers ou irréguliers :

	Convexe	Concave
Régulier	Tous les angles sont inférieurs à 180^o Tous les côtés sont égaux	Un ou plusieurs angles sont supérieurs à 180^o Tous les côtés sont égaux
Irrégulier	Tous les angles sont inférieurs à 180^o Les côtés ne sont pas égaux	Un ou plusieurs angles sont supérieurs à 180^o Les côtés ne sont pas égaux

Figures

Voici les quatre types représentés en figures :

	Convexe	Concave
Régulier
Irrégulier

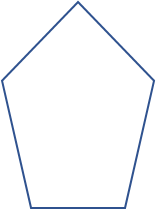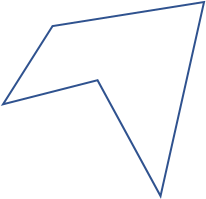Polygone complexe

Les quatre ci-dessus sont appelés polygones simples, et en plus il existe des polygones complexes où les lignes se croisent également.

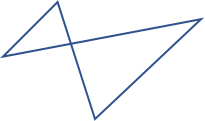
Polygone complexe

Somme des angles d’un polygone

La somme des angles d’un polygone peut être calculée avec la formule suivante :

$$ Somme\ des\ angles = (Nombre\ de\ côtés - 2) \cdot 180 \\[12pt] \Leftrightarrow \\[12pt] \sum \alpha = (n-2)\cdot 180 $$

Si vous utilisez cette formule pour des polygones concaves, souvenez-vous qu’elle calcule la somme des angles intérieurs.

Aire

Pour les polygones convexes réguliers, il existe une formule qui permet de calculer l’aire :

$$ Aire=\frac{1}{4} \cdot n \cdot b^2 \cdot cot \biggl( \frac{\pi}{n} \biggr) $$

Où $n$ = nombre de côtés et $b$ = longueur du côté.

Si vous avez un pentagone avec une longueur de côté de 8, cela ressemblerait à ceci :

$$ Aire=\frac{1}{4} \cdot 5 \cdot 8^2 \cdot cot \biggl( \frac{\pi}{5} \biggr) \Leftrightarrow $$

$$ Aire=\frac{5 \cdot 64 \cdot 1.376382}{4} \Leftrightarrow $$

$$ Aire = 110.11 $$

Cot est cotangente (cosinus divisé par sinus). Si votre calculatrice n’a pas ce bouton, vous pouvez le calculer ainsi :

$$ cot \biggl( \frac{\pi}{n} \biggr)= \frac{cos \biggl( \frac{\pi}{n} \biggr)}{sin \biggl( \frac{\pi}{n} \biggr)} $$

Périmètre

Il n’y a pas de règles particulières pour le périmètre. Il suffit de trouver les longueurs des côtés et de les additionner.

En général, lorsque vous calculez des polygones et qu’il n’existe pas de formule, il s’agit de diviser la figure en formes que vous pouvez calculer.

Ici, il est utile d’avoir une bonne maîtrise de la trigonométrie.

Pentagramme

Un polygone complexe bien connu que la plupart des gens peuvent dessiner facilement est un pentagramme.

Il peut être dessiné en un seul trait sans lever le crayon.

Pentagramme

Le pentagramme est un polygone complexe parce que les lignes se croisent.

Le pentagramme montré est également régulier car tous les côtés sont de même longueur.

Décagone (Polygone à dix côtés)

Le décagone ci-dessous n’est pas un polygone complexe. C’est un polygone concave régulier.

Décagone

Il pourrait aussi être dessiné de manière irrégulière. La somme des angles intérieurs du polygone à dix côtés est 1440^o

Noms des polygones

Nombre de côtés	Nom	Somme des angles
3	Trigon	180^o
4	Tétragone	360^o
5	Pentagone	540^o
6	Hexagone	720^o
7	Heptagone	900^o
8	Octogone	1.080^o
9	Ennéagone	1.260^o
10	Décagone	1.440^o
11	Hendécagone	1.620^o
12	Dodécagone	1.800^o
13	Tridécagone	1.980^o
14	Tétradécagone	2.160^o
15	Pentadécagone	2.340^o
16	Hexadécagone	2.520^o
17	Heptadécagone	2.700^o
18	Octadécagone	2.880^o
19	Ennéadécagone	3.060^o
20	Icosagone	3.240^o
50	Pentacontagone	8.640^o
1.000	Chiliagone	179.640^o
10.000	Myriagone	1.799.640^o