Continuité
Lorsqu’on parle du comportement des fonctions, l’un des concepts les plus importants est la continuité. La continuité décrit si une fonction varie de manière régulière ou si des sauts, des trous ou des changements brusques apparaissent dans le graphe. Une fonction continue peut être tracée sans lever le crayon du papier.
Définition de la continuité
Une fonction \( \large f(x) \) est continue en un point \( \large x = a \) si la limite de la fonction en ce point est égale à la valeur de la fonction. Cela s’écrit :
$$ \large \lim_{x \to a} f(x) = f(a) $$
Pour qu’une fonction soit continue en un point, trois conditions doivent être remplies :
- La fonction est définie en \( \large a \)
- La limite \( \large \lim_{x \to a} f(x) \) existe
- Les deux valeurs sont égales
Si l’une de ces conditions n’est pas remplie, la fonction n’est pas continue en ce point.
Types de discontinuité
Il existe plusieurs façons pour une fonction d’être discontinue. Les principaux types sont :
| Type | Description |
|---|---|
| Discontinuité par saut | La fonction passe brusquement d’une valeur à une autre. |
| Trou | La limite existe, mais la fonction n’est pas définie en ce point. |
| Discontinuité infinie | La fonction croît sans limite en ce point (par exemple, près d’une asymptote verticale). |
Ces types se remarquent clairement sur le graphe et aident à comprendre le comportement général de la fonction. L’exemple ci-dessous montre une discontinuité par saut :
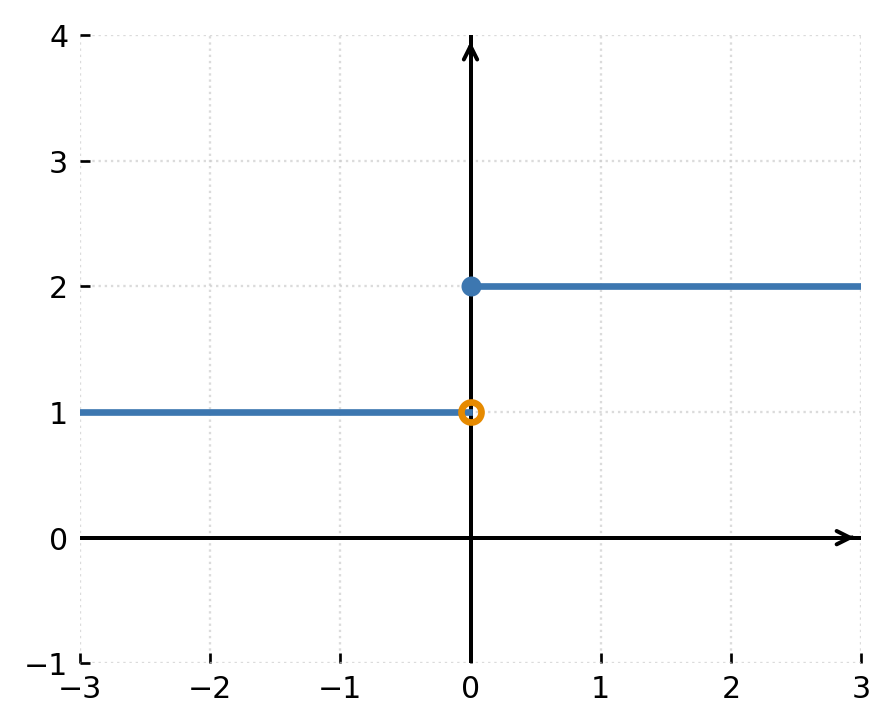
Exemples
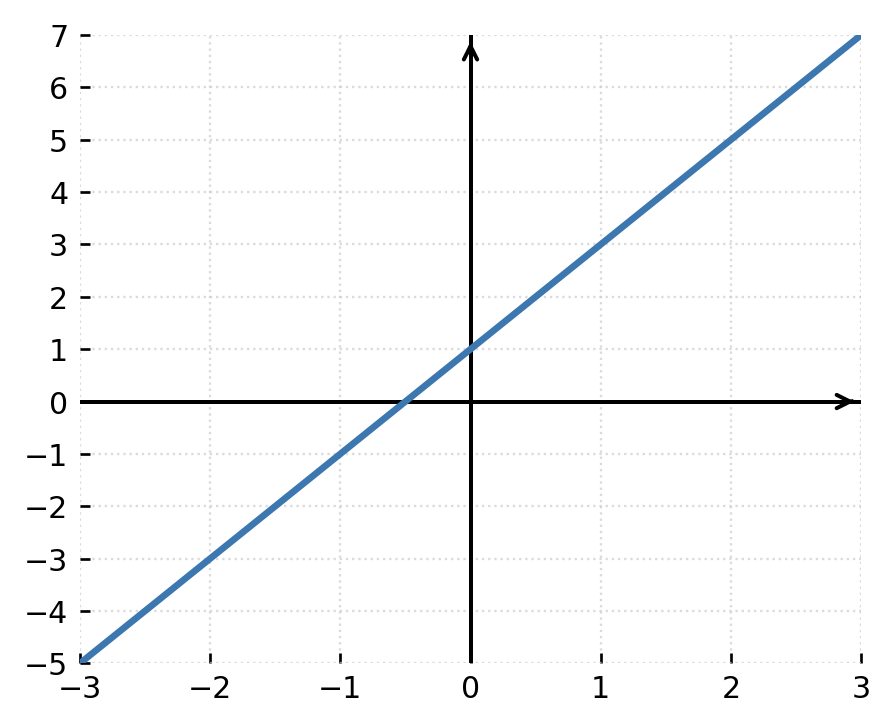
1 : La fonction \( \large f(x) = 2x + 1 \) est continue partout, car on peut substituer n’importe quelle valeur de x sans interrompre le graphe.
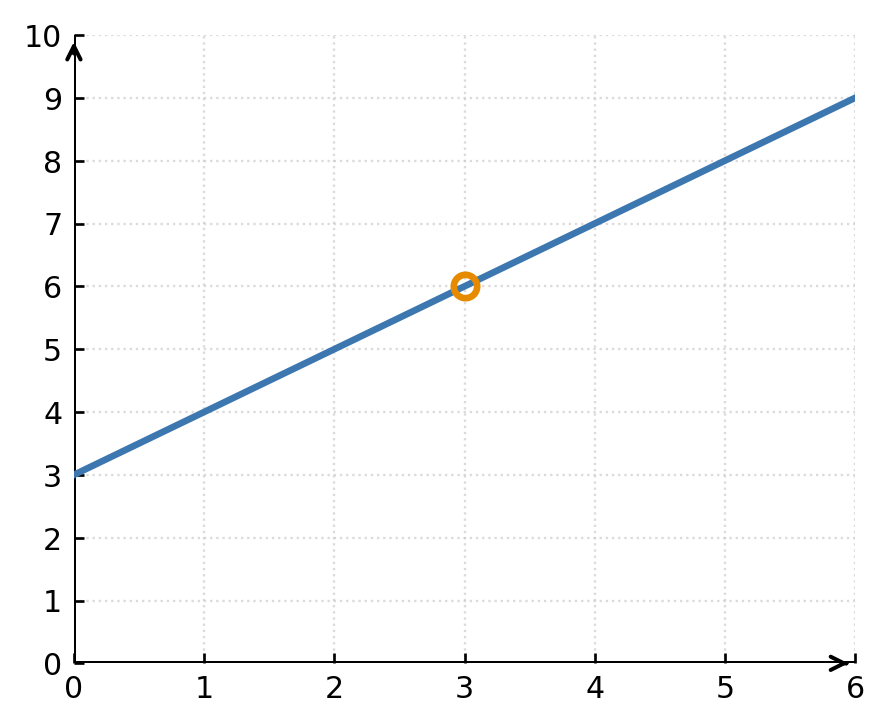
2 : La fonction
$$ \large f(x) = \frac{x^2 - 9}{x - 3} $$
n’est pas définie en \( \large x = 3 \), mais la limite en ce point existe :
$$ \large \lim_{x \to 3} \frac{x^2 - 9}{x - 3} = 6 $$
Le graphe présente donc un trou au point (3, 6). La fonction peut être rendue continue en définissant \( \large f(3) = 6 \).
Continuité sur un intervalle
Une fonction est dite continue sur un intervalle si elle est continue en chaque point de cet intervalle. Les fonctions polynomiales, exponentielles, logarithmiques et trigonométriques sont des exemples de fonctions continues partout où elles sont définies.
La continuité est une condition essentielle de nombreux théorèmes de l’analyse, notamment le théorème des valeurs intermédiaires et ceux relatifs à la dérivabilité.
Importance en analyse
La continuité garantit que de petits changements de x entraînent de petits changements de f(x). Cette propriété est essentielle pour définir la dérivée, qui décrit la pente et les variations locales de la fonction. La continuité est donc une pierre angulaire de toute l’analyse.