Intégrale définie

L’intégrale définie est utilisée pour calculer la quantité totale d’une fonction entre deux points. Alors que l’intégrale indéfinie décrit toutes les primitives, l’intégrale définie donne un nombre représentant la valeur accumulée — souvent une aire.

 

 

Définition

L’intégrale définie d’une fonction \( \large f(x) \) de \( \large a \) à \( \large b \) est définie comme la limite de la somme de nombreux petits rectangles sous la courbe :

 

$$ \large \int_a^b f(x)\,dx \;=\; \lim_{n \to \infty} \sum_{i=1}^{n} f(x_i)\,\Delta x $$

 

Chaque terme de la somme représente l’aire d’un petit rectangle de hauteur \( \large f(x_i) \) et de largeur \( \large \Delta x \). Lorsque le nombre de rectangles augmente, l’approximation devient plus précise et, à la limite, on obtient l’aire exacte.

 

 

Interprétation géométrique

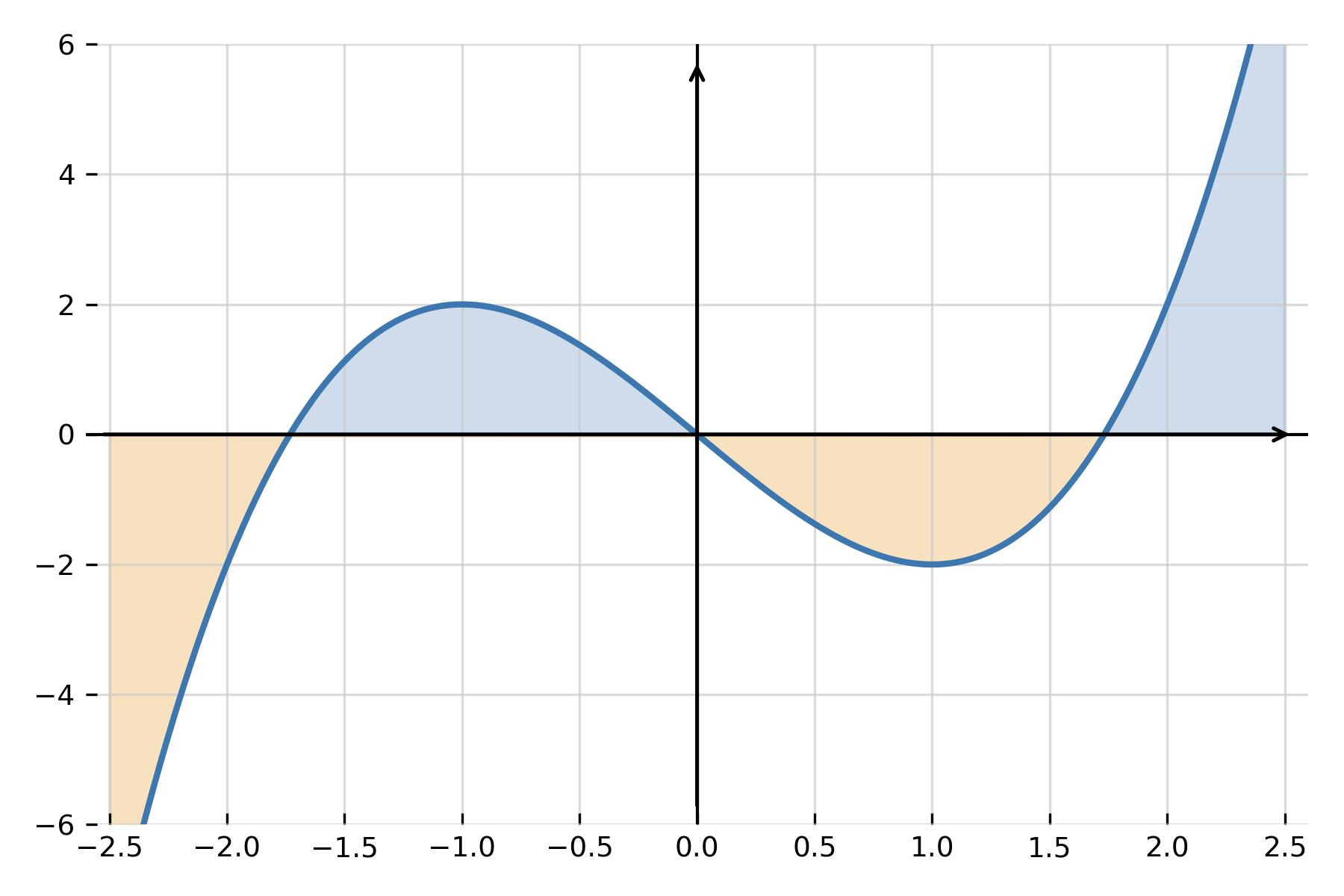
Si \( \large f(x) \ge 0 \) sur l’intervalle, l’intégrale définie représente l’aire comprise entre la courbe et l’axe des abscisses. Si la fonction traverse l’axe des x, les zones situées en dessous sont comptées comme négatives, de sorte que l’intégrale indique l’aire nette.

 

 

 

Théorème fondamental

Il existe un lien étroit entre les primitives et les intégrales définies. Si \( \large F \) est une primitive de \( \large f \), le théorème fondamental du calcul intégral énonce :

 

$$ \large \int_a^b f(x)\,dx \;=\; F(b) - F(a) $$

 

Cela signifie qu’on peut calculer une intégrale définie sans utiliser de sommes de Riemann. Il suffit de trouver une primitive et de soustraire les valeurs de la fonction aux deux bornes.

 

 

Exemple 1 : Aire sous la courbe

Calculer l’aire sous \( \large f(x) = x^2 \) de \( \large x=0 \) à \( \large x=3 \) :

 

$$ \large \int_0^3 x^2\,dx \;=\; \Big[\tfrac{1}{3}x^3\Big]_0^3 \;=\; \tfrac{1}{3}\cdot 27 - 0 \;=\; 9 $$

 

L’aire sous la courbe est donc de 9 unités.

 

 

Exemple 2 : Parties négatives et positives

Calculer \( \large \int_{-1}^{2} (x-1)\,dx \) :

 

$$ \large \int_{-1}^{2} (x-1)\,dx \;=\; \Big[\tfrac{1}{2}x^2 - x\Big]_{-1}^{2} \;=\; \big(2 - 2\big) - \big(\tfrac{1}{2} - (-1)\big) = -\tfrac{3}{2} $$

 

L’intégrale est négative parce que la fonction se situe sous l’axe des x sur une partie de l’intervalle. L’intégrale définie mesure donc l’accumulation nette, et non simplement la somme des aires positives.

 

 

Signe et quantité accumulée

Une intégrale positive signifie que la fonction est en moyenne au-dessus de l’axe des x sur l’intervalle. Une intégrale négative indique le contraire. En physique et en économie, cela est interprété comme un excédent ou un déficit d’une quantité totale.

 

 

Interprétation graphique

L’intégrale définie peut être comprise comme la somme des aires signées. On peut donc la visualiser comme l’aire entre la courbe et l’axe des x, où les aires situées en dessous de l’axe sont soustraites.

 

 

Résumé

L’intégrale définie donne un nombre qui représente le changement total, la quantité accumulée ou l’aire nette d’une fonction entre deux bornes. Elle peut être obtenue soit géométriquement comme une aire, soit algébriquement à l’aide des primitives et du théorème fondamental.