Applications du calcul intégral
Les intégrales ne servent pas seulement à calculer des aires, mais aussi dans de nombreux contextes où il faut additionner de petites contributions pour obtenir une grandeur totale. En physique, en économie et en géométrie, les intégrales fournissent un outil mathématique précis pour mesurer la croissance totale, l’énergie, la masse, la distance ou le volume.
Aire entre deux courbes
L’une des applications les plus courantes consiste à trouver l’aire comprise entre deux fonctions \( \large f(x) \) et \( \large g(x) \). Si \( \large f(x) \ge \large g(x) \) sur l’intervalle \([ \large a,\large b ]\), l’aire se calcule comme la différence entre les deux :
$$ \large A \;=\; \int_a^b \big(f(x) - g(x)\big)\,dx $$
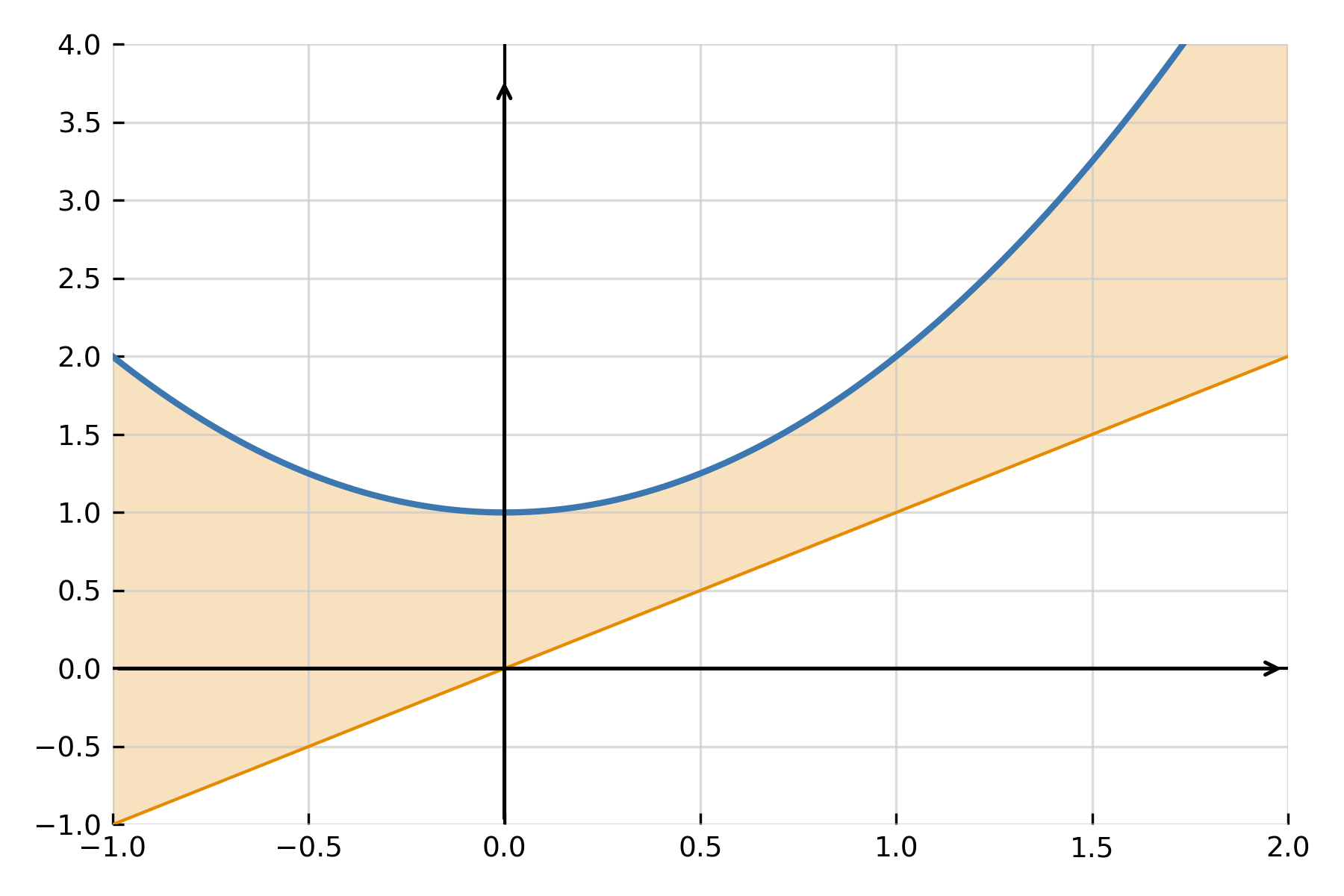
L’intégrale mesure exactement la distance verticale entre les courbes pour chaque \( \large x \) et additionne cette distance sur tout l’intervalle. Si les courbes se croisent, l’intervalle est découpé en parties où l’on prend à chaque fois la différence positive.
Volume des solides de révolution
Lorsqu’une fonction est tournée autour de l’axe des x, elle forme un solide tridimensionnel. Le volume peut être trouvé en additionnant les aires des sections transversales (disques) le long de l’axe :
$$ \large V \;=\; \pi \int_a^b \big(f(x)\big)^2\,dx $$
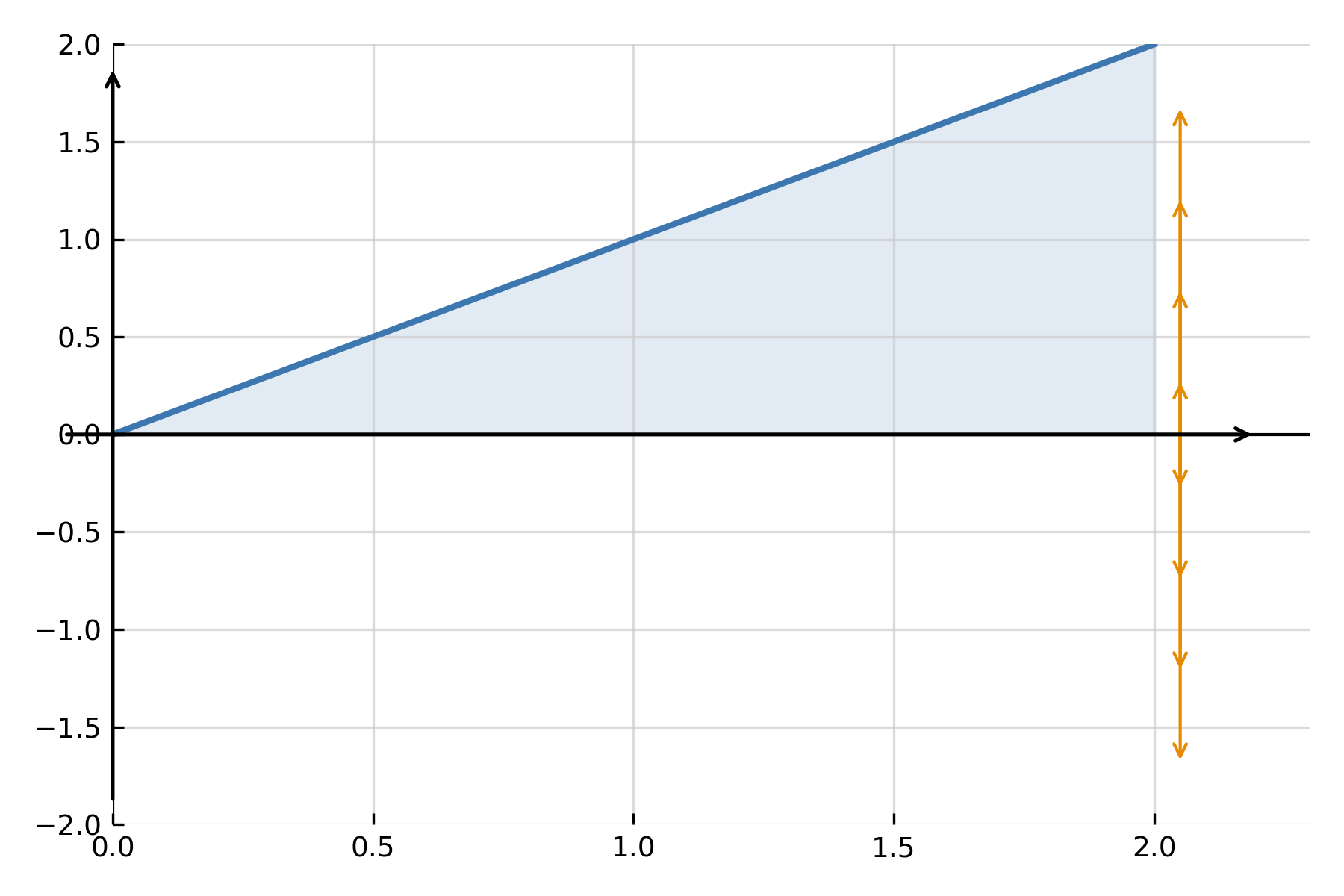
Ici, \( \large f(x) \) est le rayon de la fonction tournée au point \( \large x \). L’intégrale additionne une infinité de petits disques qui, ensemble, forment le volume total.
Exemple : Solide de révolution
Trouver le volume du solide formé en tournant \( \large f(x)=x \) autour de l’axe des x de \( \large x=0 \) à \( \large x=2 \) :
$$ \large V \;=\; \pi \int_0^2 x^2\,dx \;=\; \pi \Big[\tfrac{1}{3}x^3\Big]_0^2 \;=\; \tfrac{8}{3}\pi $$
Cela correspond au volume d’un cône de hauteur 2 et de rayon 2.
Travail et énergie
En physique, les intégrales sont utilisées pour calculer le travail lorsqu’une force varie avec la position. Le travail \( \large W \) est la somme des petites contributions de force \( \large F(x)\,dx \) :
$$ \large W \;=\; \int_a^b F(x)\,dx $$
Si la force est constante, cela se réduit à \( \large W = F \cdot s \), mais l’intégrale permet le calcul lorsque la force change au cours du mouvement.
Mouvement et distance parcourue
Lorsque la fonction de vitesse \( \large v(t) \) d’un objet est connue, l’intégrale de \( \large v(t) \) donne la distance parcourue :
$$ \large s \;=\; \int_{t_1}^{t_2} v(t)\,dt $$
Si la vitesse peut être négative (mouvement vers l’arrière), il faut intégrer en tenant compte du signe. Si l’on veut la distance totale sans se soucier de la direction, on utilise \( \large \int |v(t)|\,dt \) à la place.
Applications économiques et biologiques
Les intégrales sont également utilisées pour calculer la croissance accumulée, la consommation ou le revenu au fil du temps. En économie, \( \large f(x) \) peut représenter une fonction marginale, par exemple le revenu par unité, et l’intégrale donne le revenu total. En biologie, les intégrales servent à mesurer la biomasse totale, l’apport énergétique ou la quantité de matière d’une population.
Valeur moyenne d’une fonction
La valeur moyenne d’une fonction sur un intervalle se trouve en prenant l’aire totale et en la divisant par la longueur de l’intervalle :
$$ \large f_{\text{moy}} \;=\; \frac{1}{b-a}\int_a^b f(x)\,dx $$
Cette formule est utilisée en statistique, en physique et en analyse pour trouver les valeurs moyennes des fonctions continues.
Lorsqu’une intégrale ne peut pas être calculée analytiquement, on peut utiliser des méthodes numériques telles que la méthode des rectangles, la méthode des trapèzes ou la règle de Simpson pour obtenir une valeur approchée. Ces méthodes sont décrites dans la section Méthodes numériques.
Résumé
Les intégrales servent à calculer des aires, des volumes, de l’énergie, du travail et bien d’autres grandeurs. Toutes ces applications ont en commun que l’intégrale additionne de petites parties pour obtenir une quantité totale. Ainsi, le calcul intégral constitue un outil essentiel pour décrire et calculer les relations dans la nature, la technologie et l’économie.