Calcul intégral
Le calcul intégral consiste à additionner de petites contributions pour obtenir une grandeur totale. Alors que le calcul différentiel mesure les changements instantanés (\( \large \text{pentes} \)), le calcul intégral mesure des grandeurs accumulées telles que l’aire, la distance, la croissance totale ou l’énergie. Les deux branches sont étroitement liées : dériver et intégrer sont des processus inverses.
Qu’est-ce que le calcul intégral
Lorsqu’une grandeur varie progressivement, on peut imaginer diviser le processus en de nombreuses petites parties et les additionner. C’est l’essence du calcul intégral : la somme de « petites parties » devient une grandeur globale. En pratique, cela s’exprime à l’aide des intégrales.
Interprétation géométrique
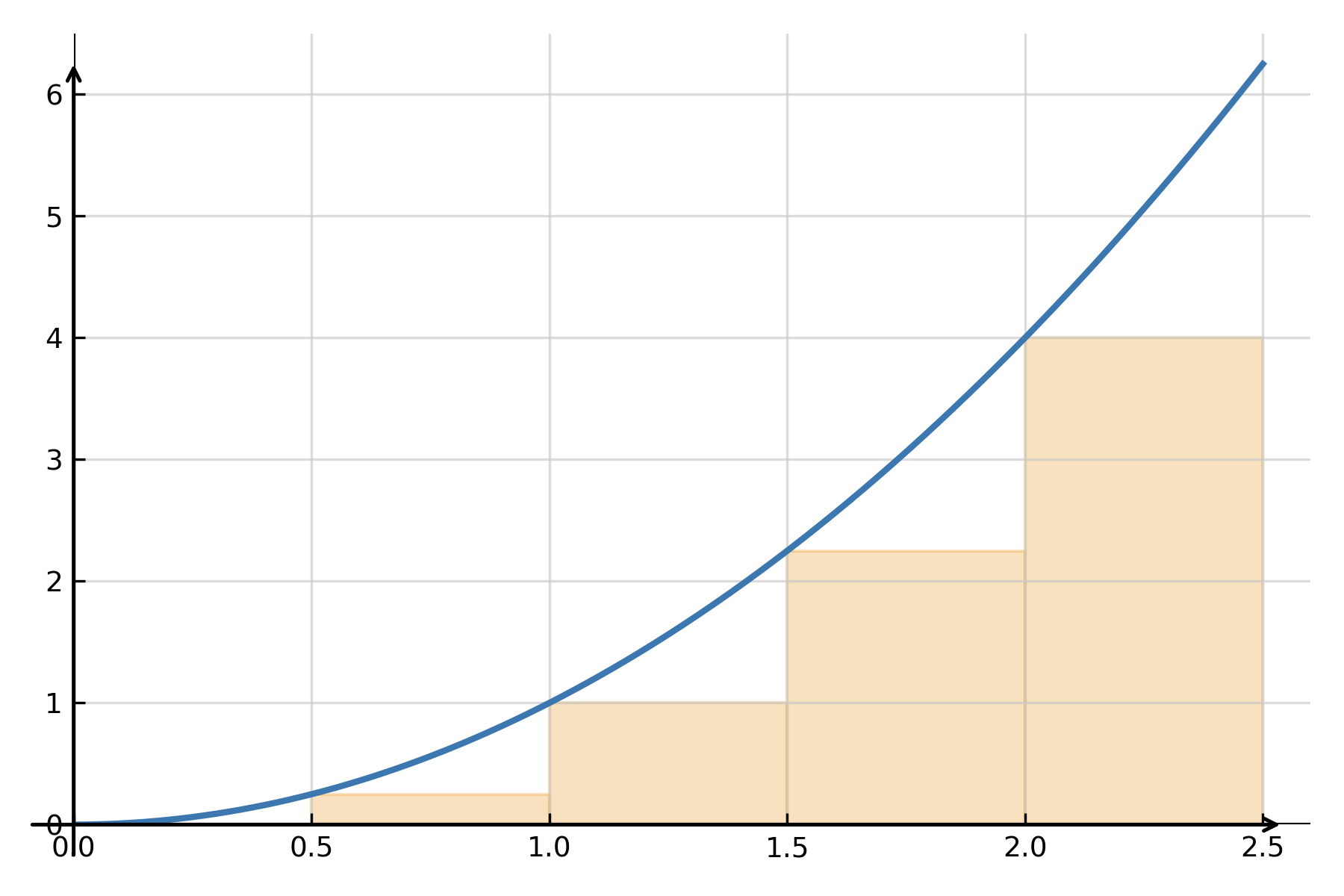
Une interprétation classique est l’aire sous la courbe d’une fonction non négative \( \large f(x) \) entre \( \large x=a \) et \( \large x=b \). On peut approximer l’aire en divisant l’intervalle en rectangles étroits, en calculant leurs aires et en les additionnant. Lorsque la largeur tend vers zéro, la somme tend vers l’aire exacte.
$$ \large \text{Aire} \;=\; \lim_{n \to \infty} \sum_{i=1}^{n} f(x_i)\,\Delta x \;=\; \int_a^b f(x)\,dx $$
L’intégrale fournit donc une manière précise de mesurer une « grandeur accumulée », qu’il s’agisse d’aire, de masse, de travail ou d’une autre quantité.
Intégrale indéfinie (fonction primitive)
L’intégrale indéfinie représente la « différentiation inverse ». Si \( \large F'(x)=f(x) \), alors \( \large F \) est appelée une fonction primitive de \( \large f \), et on écrit :
$$ \large \int f(x)\,dx \;=\; F(x) + C $$
Ici \( \large C \) est une constante arbitraire. L’intégrale indéfinie représente toutes les fonctions ayant la même dérivée \( \large f \).
Intégrale définie (aire et somme)
L’intégrale définie mesure la grandeur accumulée entre deux bornes \( \large a \) et \( \large b \). Elle est définie comme la limite des sommes de Riemann :
$$ \large \int_a^b f(x)\,dx \;=\; \lim_{n\to\infty}\sum_{i=1}^{n} f(x_i)\,\Delta x $$
Si \( \large f \ge 0 \) sur l’intervalle, cela représente l’aire sous la courbe. Si \( \large f \) change de signe, l’aire sous l’axe des abscisses est comptée négativement, ce qui reflète l’accumulation nette.
Lien avec le calcul différentiel (Théorème fondamental)
Le calcul intégral et le calcul différentiel sont liés par le théorème fondamental : si \( \large f \) est continue sur \( \large [a,b] \) et si \( \large F \) est une primitive de \( \large f \), alors :
$$ \large \int_a^b f(x)\,dx \;=\; F(b) - F(a) $$
Cela signifie qu’une aire (une somme) peut être calculée à l’aide d’une fonction primitive et que la dérivation et l’intégration sont des processus inverses.
Exemples
1. Aire sous une fonction simple
Déterminer \( \large \int_0^2 x\,dx \). Une primitive est \( \large F(x)=\tfrac{1}{2}x^2 \), donc :
$$ \large \int_0^2 x\,dx \;=\; \Big[\tfrac{1}{2}x^2\Big]_0^2 \;=\; \tfrac{1}{2}\cdot 4 - 0 \;=\; 2 $$
2. Distance accumulée à partir d’une fonction de vitesse
Si la vitesse d’une voiture est \( \large v(t)=3t \) (m/s), la distance parcourue de \( \large t=0 \) à \( \large t=4 \) est :
$$ \large s \;=\; \int_0^4 v(t)\,dt \;=\; \int_0^4 3t\,dt \;=\; \Big[\tfrac{3}{2}t^2\Big]_0^4 \;=\; 24\ \text{m} $$
Cela montre que l’aire sous la courbe de vitesse correspond à la distance totale parcourue.
Pourquoi deux types d’intégrales
L’intégrale indéfinie (fonction primitive) est un outil pour trouver des formules et travailler algébriquement, tandis que l’intégrale définie \( \large \text{mesure} \) une grandeur concrète sur un intervalle. Le théorème fondamental permet de traduire entre ces deux perspectives.
Résumé
Le calcul intégral consiste à additionner de petites contributions pour former une grandeur totale. Géométriquement, les intégrales sont interprétées comme des aires ; physiquement, comme une masse, un travail ou une distance accumulée. Grâce au théorème fondamental, les intégrales définies peuvent être calculées à l’aide de fonctions primitives, faisant du calcul intégral le processus « inverse » naturel de la dérivation.