Trigonometría
La trigonometría es el estudio de las relaciones entre los lados y los ángulos de un triángulo y del cálculo de las cantidades desconocidas a partir de las que conoces.
La trigonometría plana trata de las relaciones en un triángulo plano.
Con base en el círculo unitario y el conocimiento de las funciones y relaciones trigonométricas, es posible calcular casi todas las figuras geométricas, incluidas las espaciales.

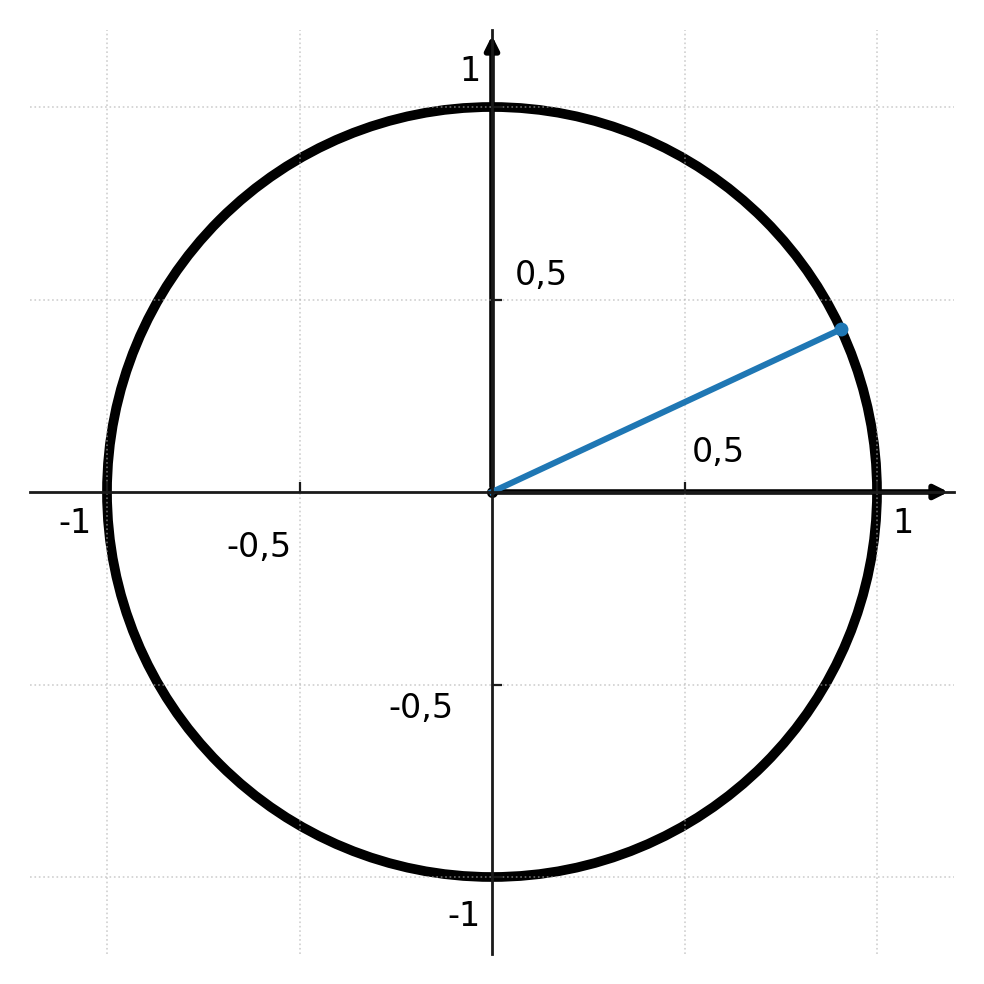
Si imaginas el círculo unitario dibujado en un sistema de coordenadas, el centro del círculo está en (0,0) y tiene un radio de 1.
A partir del círculo unitario se pueden definir tres funciones, coseno, seno y tangente, que se utilizan para calcular los ángulos y lados de los triángulos.
La circunferencia del círculo unitario es \( \large 2 \cdot \pi \).
El área del círculo unitario es \( \large \pi \).
Funciones y relaciones
Existen en total seis funciones trigonométricas. En un triángulo rectángulo se definen de la siguiente manera:
| Función | Definición |
|---|---|
| Seno (sin) | \( \Large \sin(v) = \tfrac{\text{cateto opuesto}}{\text{hipotenusa}} \) |
| Coseno (cos) | \( \Large \cos(v) = \tfrac{\text{cateto adyacente}}{\text{hipotenusa}} \) |
| Tangente (tan) | \( \Large \tan(v) = \tfrac{\text{cateto opuesto}}{\text{cateto adyacente}} \) |
| Cotangente (cot) | \( \Large \cot(v) = \tfrac{\text{cateto adyacente}}{\text{cateto opuesto}} \) |
| Secante (sec) | \( \Large \sec(v) = \tfrac{\text{hipotenusa}}{\text{cateto adyacente}} \) |
| Cosecante (csc) | \( \Large \csc(v) = \tfrac{\text{hipotenusa}}{\text{cateto opuesto}} \) |
Para la geometría habitual, las tres primeras son las más importantes. También es importante poder usar las relaciones del seno y del coseno.
Línea, punto y ángulo de referencia
Si trazas una línea desde el centro (0,0) hasta un punto aleatorio en el arco del círculo, la línea formará un ángulo con el eje x del sistema de coordenadas.
El punto que elegiste en el arco del círculo se llama punto de referencia. La línea que trazaste se llama línea de referencia, y el ángulo que se forma con el eje x se llama ángulo de referencia.
Si conoces el ángulo de un triángulo, puedes dibujarlo en el círculo, y el punto de referencia será la base para tu cálculo del triángulo.
Trigonometría esférica
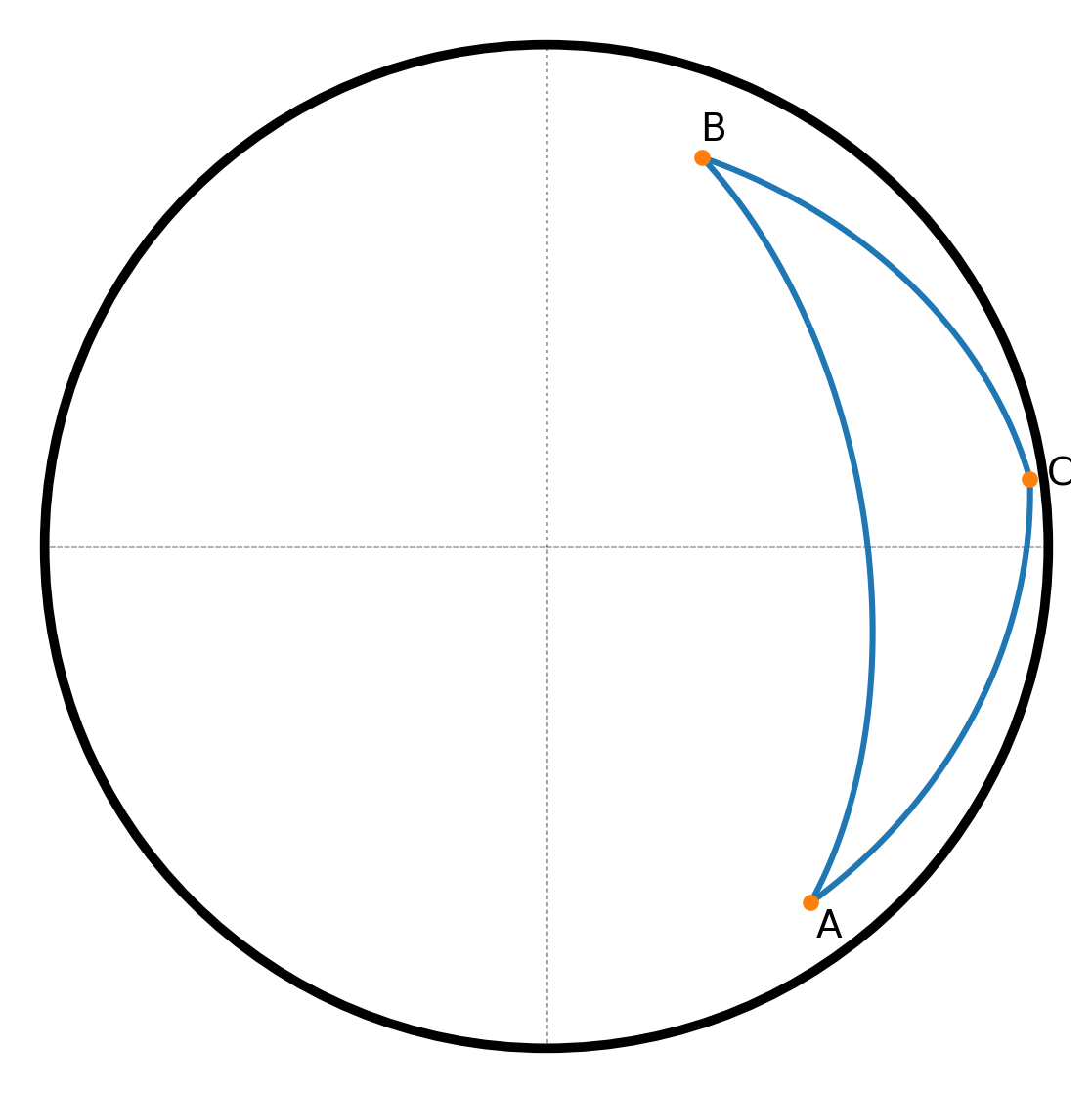
La trigonometría esférica trata de triángulos y otras figuras geométricas en la superficie de una esfera.
Así como tenemos el círculo unitario con radio 1 en la trigonometría plana, se puede imaginar una esfera unitaria con radio 1.
Un triángulo esférico se forma por tres arcos de círculos máximos en la superficie de la esfera. Con la ayuda de las funciones trigonométricas se pueden calcular las interdependencias entre lados y ángulos en dichos triángulos.
La trigonometría esférica se ha desarrollado especialmente para su uso en la navegación y la astronomía.