Seno y coseno

Si dibujas un ángulo en el círculo unitario, puedes leer el coseno y el seno en la circunferencia del círculo unitario como un punto en el sistema de coordenadas.

El resultado siempre estará entre -1 y 1, porque el punto siempre se encuentra en el círculo con radio 1.

En la figura, se ha dibujado un ángulo de 25 grados en el círculo unitario, y podemos leer el punto de intersección en los ejes x e y.

 

 

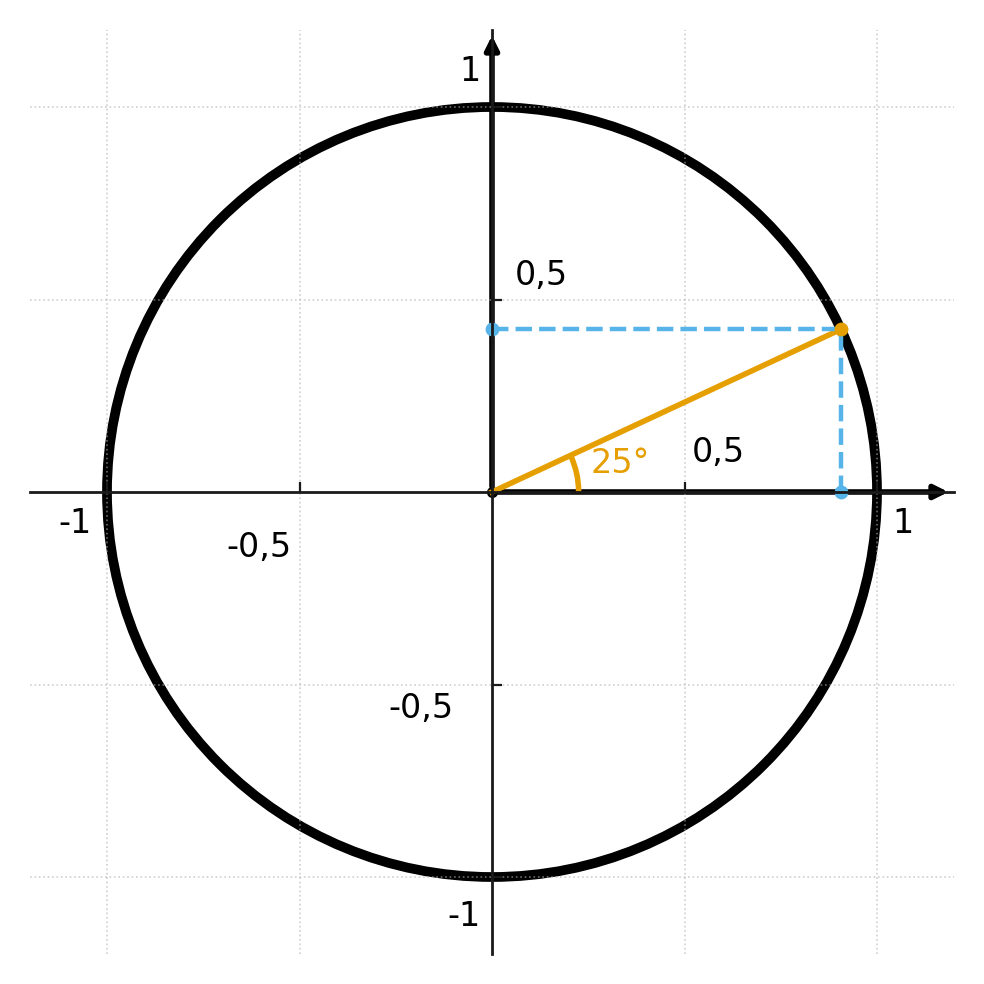
Recuerda que las coordenadas siempre se leen como \( \large (x,y) \), lo que corresponde a \( \large (coseno, seno) \).

El coseno y el seno son, por lo tanto, el par de coordenadas del punto de referencia – el punto donde el ángulo corta el círculo unitario.

El ángulo en la figura es de 25 grados, y si se pudiera leer con la suficiente precisión, se vería que:

 

$$ sen(v) \approx 0.906 $$

$$ cos(v) \approx 0.423 $$

 

Por supuesto, no es posible leer exactamente en el círculo unitario, y normalmente se utilizan los botones de coseno y seno en la calculadora.

 

Funciones inversas

Si conoces el coseno o el seno de un ángulo, pero no el ángulo mismo, puedes calcular al revés con las funciones inversas. Estas se llaman arccos y arcsin (o se escriben como cos^-1 y sen^-1).

Las funciones inversas también se encuentran en una calculadora, normalmente en la misma tecla que las funciones ordinarias.

 

Supongamos que sabes que cos(A) = 0.906, pero no conoces el ángulo. Entonces puedes encontrarlo así:

 

$$ cos^{-1}(0.906) \approx 25^\circ $$

 

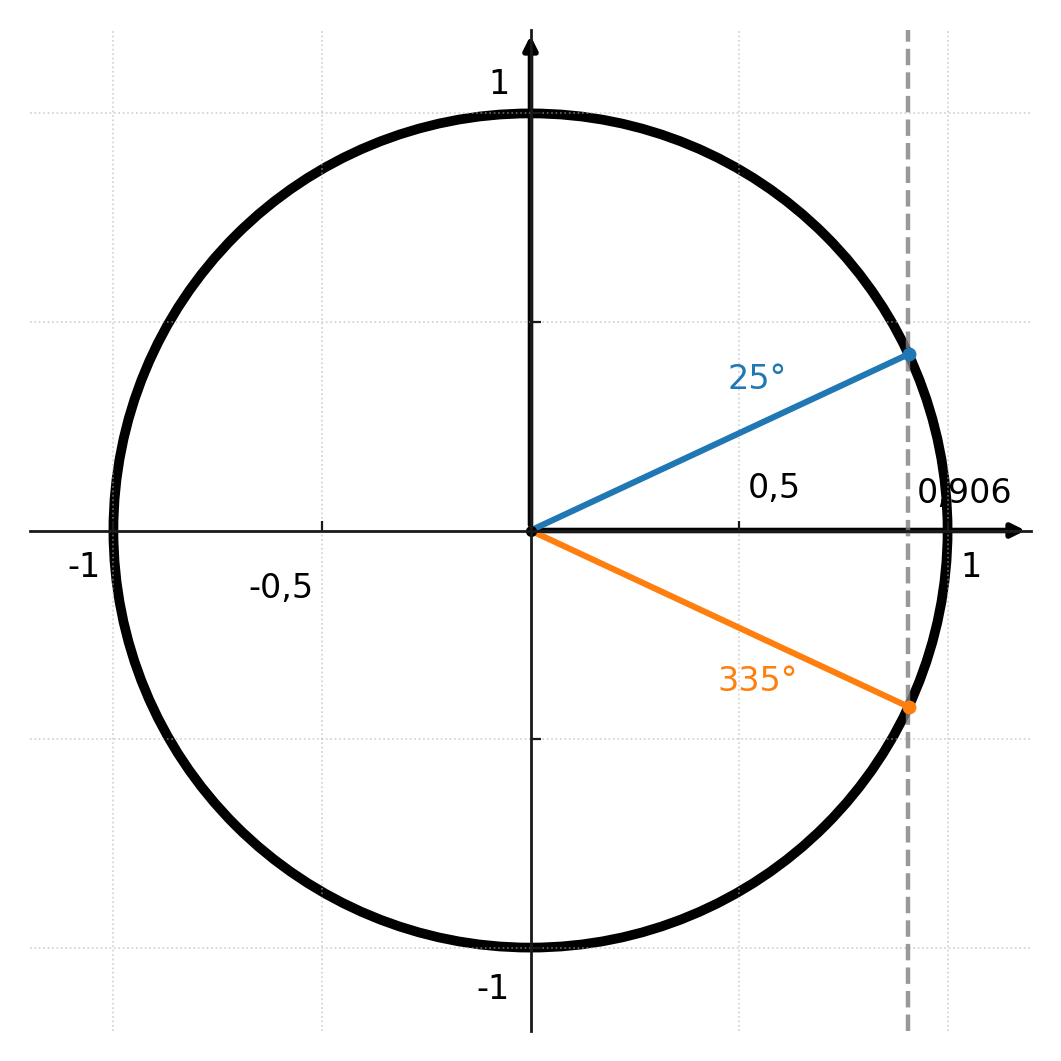
Ten en cuenta que las funciones inversas no siempre dan una solución única. Por ejemplo, cos(v) = 0.906 puede corresponder tanto a un ángulo de 25° como a un ángulo de 335° (-25°).

Para poder usar las funciones como funciones inversas únicas, se restringe su definición:

 

• Arccos normalmente se restringe al intervalo \(0^\circ \leq v \leq 180^\circ\) (\(0 \leq v \leq \pi\) rad)
• Arcsin normalmente se restringe al intervalo \(-90^\circ \leq v \leq 90^\circ\) (\(-\tfrac{\pi}{2} \leq v \leq \tfrac{\pi}{2}\) rad)

 

Esto significa que la solución de 335° no aparece, y que arcsin siempre devuelve ángulos en el primer o cuarto cuadrante.

 

 

 

 

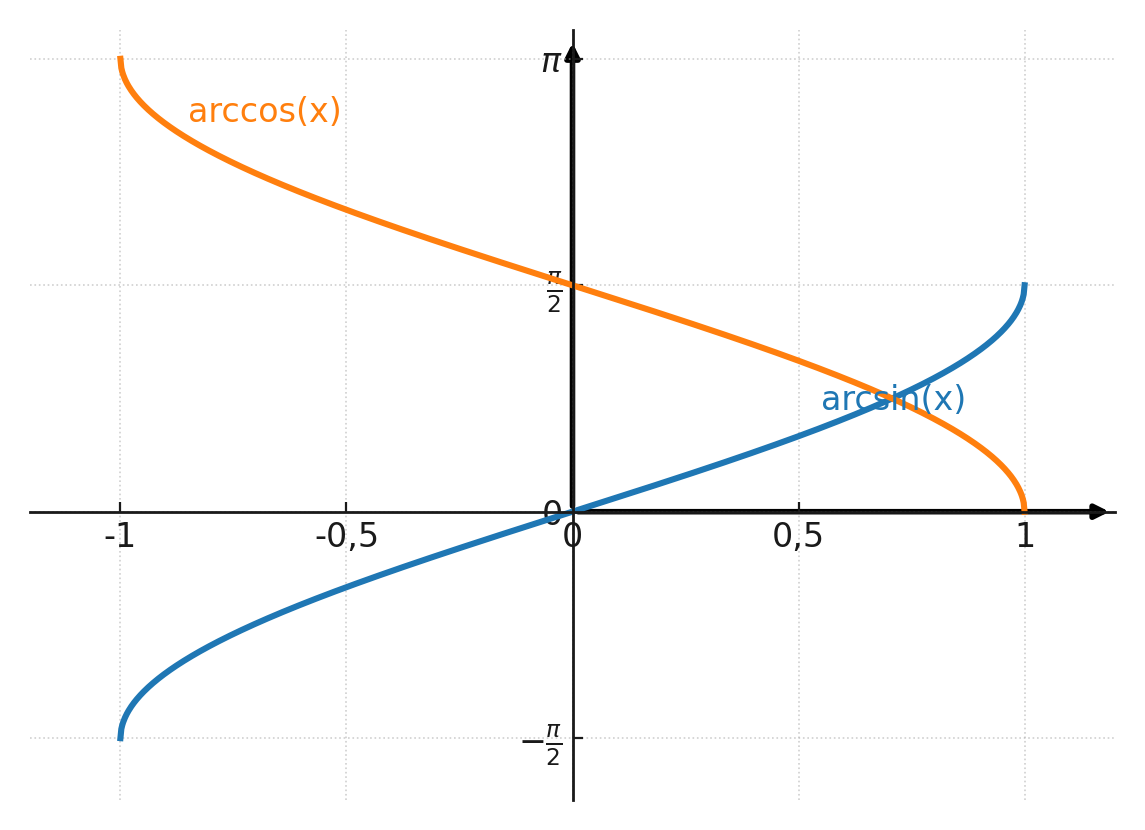
Las dos funciones inversas están dibujadas en el sistema de coordenadas. Ten en cuenta que el eje y está en radianes y no en grados.

Si se lee en la curva de arccos en x = 0.906, se obtiene 0.44 rad, lo que corresponde a 25°.

 

 

 

Radianes y Grados

Para convertir entre radianes y grados se usa la fórmula:

 

$$ \text{grados} = \text{radianes} \cdot \frac{180^\circ}{\pi} $$

$$ \text{radianes} = \text{grados} \cdot \frac{\pi}{180^\circ} $$

 

Ejemplo:

 

$$ 0.44 \,\text{rad} \approx 0.44 \cdot \tfrac{180^\circ}{\pi} \approx 25^\circ $$