Polígonos
Un polígono es una "figura de muchos lados", es decir, una figura con muchos lados.
¿Qué significa entonces "muchos lados"?
Abarca todas las figuras con lados, incluidas los triángulos y los cuadriláteros. Les hemos dado nombres propios en lugar de decir simplemente "un polígono con tres lados".
Así que polígono es un término general para figuras con varios lados.
Diferentes polígonos
Los polígonos pueden ser convexos o cóncavos y regulares o irregulares:
| Convexo | Cóncavo | |
|---|---|---|
| Regular | Todos los ángulos son menores de 180o Todas las lados son iguales |
Uno o más ángulos son mayores de 180o Todas las lados son iguales |
| Irregular | Todos los ángulos son menores de 180o Los lados no son iguales |
Uno o más ángulos son mayores de 180o Los lados no son iguales |
Figuras
Aquí se muestran los cuatro tipos como figuras:
| Convexo | Cóncavo | |
|---|---|---|
| Regular |
 |
 |
| Irregular |
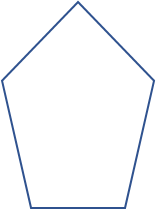 |
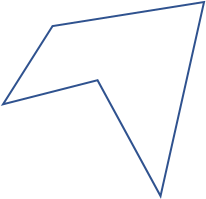 |
Polígono complejo
Los cuatro anteriores se llaman polígonos simples, y además existen polígonos complejos donde las líneas también se cruzan.
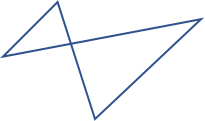
Suma de ángulos en polígonos
La suma de los ángulos en un polígono se puede calcular con la siguiente fórmula:
$$ Suma\ de\ ángulos = (Número\ de\ lados - 2) \cdot 180 \\[12pt] \Leftrightarrow \\[12pt] \sum \alpha = (n-2)\cdot 180 $$
Si utilizas esta fórmula en polígonos cóncavos, recuerda que calcula la suma de los ángulos interiores.
Área
Para los polígonos convexos regulares existe una fórmula que puede calcular el área:
$$ Área=\frac{1}{4} \cdot n \cdot b^2 \cdot cot \biggl( \frac{\pi}{n} \biggr) $$
Donde \(n\) = número de lados y \(b\) = longitud del lado.
Si tienes un pentágono con un lado de longitud 8, se vería así:
$$ Área=\frac{1}{4} \cdot 5 \cdot 8^2 \cdot cot \biggl( \frac{\pi}{5} \biggr) \Leftrightarrow $$
$$ Área=\frac{5 \cdot 64 \cdot 1.376382}{4} \Leftrightarrow $$
$$ Área = 110.11 $$
Cot es cotangente (coseno dividido por seno). Si tu calculadora no tiene ese botón, puedes calcularlo así:
$$ cot \biggl( \frac{\pi}{n} \biggr)= \frac{cos \biggl( \frac{\pi}{n} \biggr)}{sin \biggl( \frac{\pi}{n} \biggr)} $$
Perímetro
No hay reglas especiales para el perímetro. Solo hay que encontrar las longitudes de los lados y sumarlas.
En general, cuando calculas polígonos y no existe una fórmula, se trata de dividir la figura en formas que puedas calcular.
Aquí es útil tener una visión general de la trigonometría.
Pentagrama
Un polígono complejo muy conocido que la mayoría puede dibujar fácilmente es un pentagrama.
Se puede dibujar de un solo trazo sin levantar el lápiz.

El pentagrama es un polígono complejo porque las líneas se cruzan.
El pentagrama mostrado es también regular porque todos los lados son iguales.
Decágono (Polígono de diez lados)
El decágono de abajo no es un polígono complejo. Es un polígono cóncavo regular.

También podría dibujarse de manera irregular. La suma de los ángulos interiores del polígono de diez lados es 1440o
Nombres de los polígonos
| Número de lados | Nombre | Suma de ángulos |
|---|---|---|
| 3 | Trígono | 180o |
| 4 | Tetrágono | 360o |
| 5 | Pentágono | 540o |
| 6 | Hexágono | 720o |
| 7 | Heptágono | 900o |
| 8 | Octágono | 1.080o |
| 9 | Nonágono | 1.260o |
| 10 | Decágono | 1.440o |
| 11 | Hendecágono | 1.620o |
| 12 | Dodecágono | 1.800o |
| 13 | Tridecágono | 1.980o |
| 14 | Tetradecágono | 2.160o |
| 15 | Pentadecágono | 2.340o |
| 16 | Hexadecágono | 2.520o |
| 17 | Heptadecágono | 2.700o |
| 18 | Octadecágono | 2.880o |
| 19 | Eneadecágono | 3.060o |
| 20 | Icoságono | 3.240o |
| 50 | Pentacontágono | 8.640o |
| 1.000 | Quiliágono | 179.640o |
| 10.000 | Miriágono | 1.799.640o |