Uægte brøker og blandede tal

En brøk kaldes uægte, når tælleren er større end nævneren. Den kan feks være: $\large \frac{9}{8}$

Hvis du husker vores pizza, så ved du at $\large \frac{8}{8}$ er lig med en hel pizza.

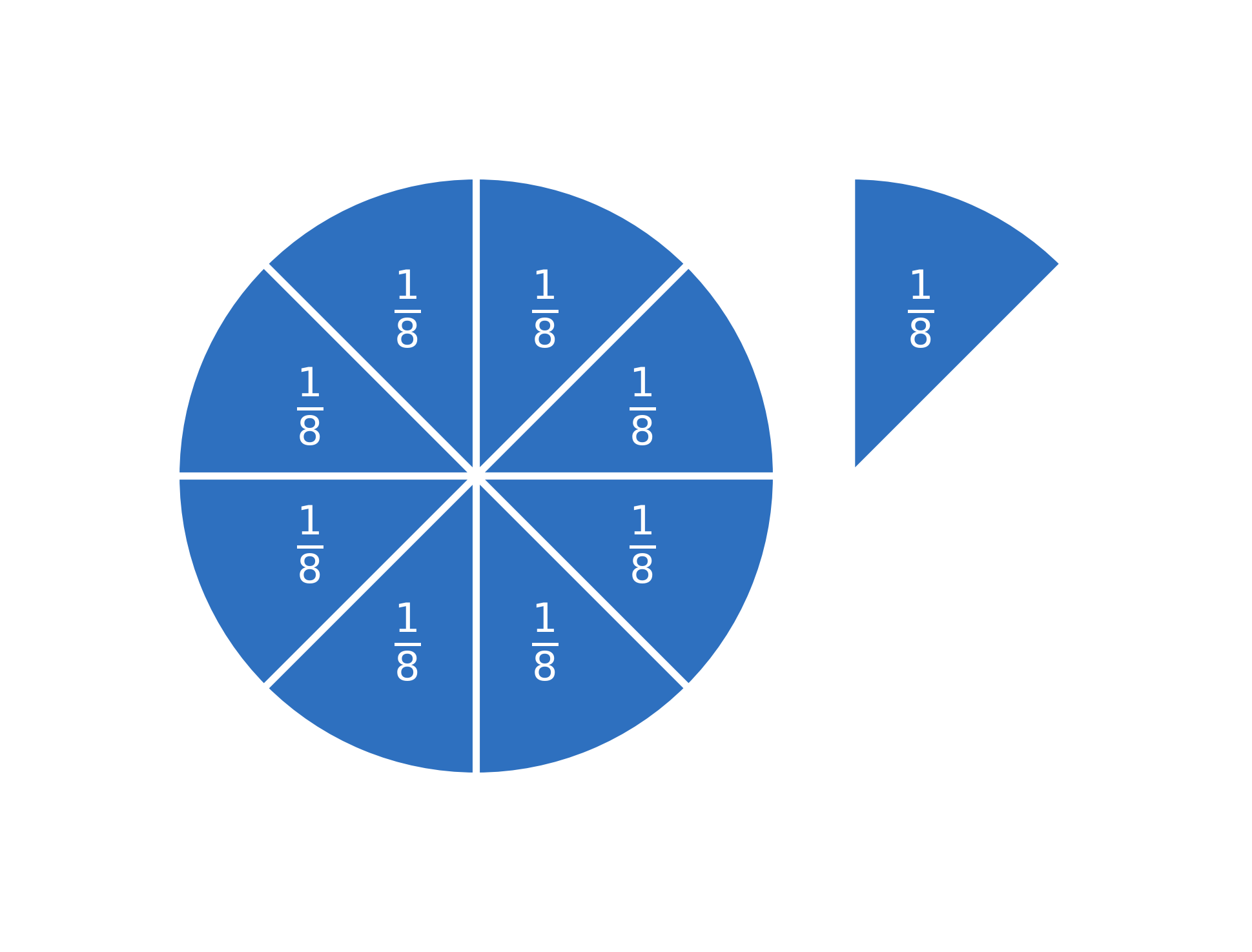
Det betyder at $\large \frac{9}{8}$ er lig med en hel pizza + et ekstra stykke, fordi:

$$ \large \frac{9}{8} \Leftrightarrow \frac{8}{8} + \frac{1}{8} $$

Det kan også skrives sådan her:

$$ \large 1+\frac{1}{8} = 1\frac{1}{8} $$

Et andet eksempel: $\large \frac{15}{7}$ er en uægte brøk. Den kan skrives som $\large 2\frac{1}{7}$

Når du skriver $\large 1+\frac{1}{8}\ $ kan du fjerne plus tegnet, så der bare står $\large 1\frac{1}{8}\ $

Det kaldes et blandet tal, fordi det både består af heltal og brøk.

Ofte omskriver man blandede tal til uægte br&os;ker, når man skal regne:

$$ \large 2\frac{1}{7} = \frac{15}{7} $$

Det er nemlig nemmere at gange og dividere uægte brøker end blandede tal.

Du kan bruge de samme regneregler på uægte brøker, som du bruger på ægte brøker.

Du skal bare huske at du ikke må aflevere en uægte brøk, som resultat på en opgave. Det skal laves om til et blandet tal eller et heltal.

Alle heltal kan skrives om til brøker. Du ved jo allerede at $\large \frac{8}{8}=1\ $. Det samme gælder for $\large \frac{1}{1}=1\ $

Det betyder at $\large 2=\frac{2}{1}\ $

Reglen er sådan her: $\large a=\frac{a}{1}\ $

Men du kan også skrive $\large 4=\frac{8}{2}\ $. Det er blot en forlængelse af $\large \frac{4}{1}\ $ Hvor der er ganget med 2 i tæller og nævner.

En brøk er jo også et divisionsstykke.

Der står: 8 divideret med 2 og det er lig med 4.